3.6 小结
复变函数的积分是定积分在复数域中的推广,两者的定义在形式上相似,但复变函数的积分实际上是复平面上的线积分.
若函数f(z)=u(x,y)+iv(x,y),C为一条光滑的有向曲线,则
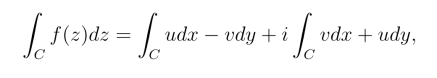
设曲线C的参数方程为z =z(t)=x(t+iy(t)),α ≤t ≤β,则
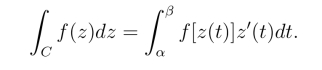
在计算复积分时,常用到下面的结果:
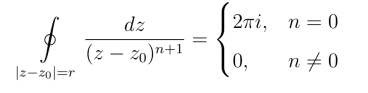
应该把它记住.
若函数f(z)在单连通域D内解析,C为D内任一简单闭曲线,则
0,这就是柯西积分定理.由柯西-古萨基本定理知上述结论对D 内任意一条封闭曲线C(不一定是简单的闭曲线)仍然成立.
将柯西-古萨基本定理推广到多连通域上,得到复合闭路定理.设D是以复闭路Γ=C+C-1 +C-2 +···+C-n 为边界的多连通域,若函数f(z)在D内及其边界Γ上解析,则f(z)沿Γ的积分为零,这时有
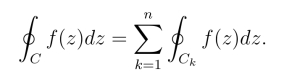
利用复合闭路定理可以把多连通域上对外边界的积分化为对内边界的积分.
复合闭路定理可以简述为：解析函数积分的积分路径作不经过被积函数奇点的连续变形,其积分值保持不变.积分函数的这种性质称为闭路变形原理,利用闭路变形原理,可以将不规则的曲线上的积分化为规则曲线(如圆周)上的积分.
柯西积分公式
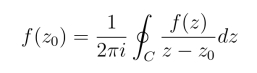
与高阶导数公式
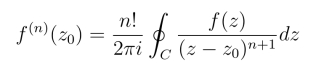
是复变函数中两个十分重要的公式,是计算积分的重要工具.
柯西积分公式的证明基于柯西-古萨基本定理,它的重要性在于一个解析函数在区域内部的值可以用它在边界上的值通过积分来表示,是研究解析函数的重要工具.例如假定解析函数f(z)在区域边界上的值为1,由柯西积分公式知f(z)在区域内的值处处等于1.但二元实函数不具有这一性质.由高阶导数公式可知解析函数的导函数仍是解析函数.
在计算沿闭曲线的积分时,一般以柯西积分定理、柯西-古萨基本定理、复合闭路定理、闭路变形原理为依据,以柯西积分公式、高阶导数公式为主要工具.由于被积函数往往形式多样,需将被积函数作适当地变形,然后再使用这些定理、公式和积分性质.对于计算沿非封闭曲线的积分,若能找到一个单连通域,使该曲线位于单连通域内,并且被积函数在单连通域内解析,则可以通过求被积函数的原函数的方法计算积分.也可以通过复积分公式(3.1.2)化为二元实函数的对坐标的曲线积分,或将曲线C写成参数方程,用式(3.1.3)计算,这时无论曲线是否封闭都可以.
关于复积分的计算将在后面的章节继续讨论.
在一个区域D内,具有二阶连续偏导数且满足拉普拉斯方程的二元函数称为区域D内的调和函数.解析函数的实部和虚部都是调和函数.
由于解析函数f(z)=u+iv的导函数仍然是解析函数,若把它的各阶导数写出来,得
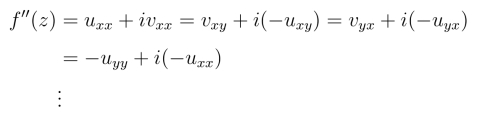
可知,u,v的四个一阶偏导数,八个二阶偏导数,··· ,任意阶的偏导数都存在而且连续,并都是调和函数.
任意两个调和函数u与v所构成的函数不一定是解析函数,还要求虚部v是实部u的共轭调和函数,也就是说满足C-R方程：ux = vy,uy = -vx.要注意u与v的位置不能颠倒.这样已知解析函数的实部或虚部就可以求出解析函数.