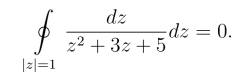3.2.1　柯西积分定理

3.2.1　柯西积分定理

由上一节复积分与实积分的关系式(3.1.2)可以看出,该复积分与路径无关的充要条件是其右端的两个对坐标的曲线积分都与路径无关.而平面上的曲线积分与路径无关的充要条件为:

若函数P(x,y)和Q(x,y)在单连通域D内具有一阶连续偏导数,L为D内分段光滑的曲线,则曲线积分在D内与路径无关(或沿D内任意闭曲线的曲线积分为零)的充分必要条件是等式

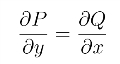
在D内恒成立.

对于式

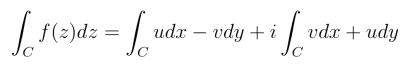
右端的两个曲线积分,上述条件等式应当分别为

这是函数f(z)在单连通域D解析的充要条件(C-R方程),那么f(z)在上述区域D内解析是否能保证它沿D内的任意简单闭路的积分为零呢?回答是肯定的,因为有下面的定理:

定理1(柯西积分定理) 若函数f(z)在简单闭曲线C上及其内部解析,则一定有

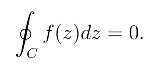
该定理的证明很麻烦,故从略.但若加附加条件“f′(z)在D内连续”,可简单证明如下:

令f(z)=u(x,y)+iv(x,y),则有

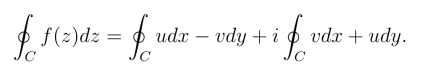
由于f′(z)在D内连续,因此ux,uy,vx,vy在D 内连续,并且满足C-R 方程

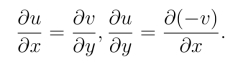
由于平面上曲线积分与路径无关的充要条件是等式(3.2.1) 成立,从而有

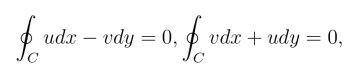
所以

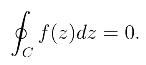
例1 计算积分

解 当|z|≤1时,由于

因此,函数z2+3z+5在单位圆周上及其内部无零点,从而被积函数在|z| =1及其内部解析,由柯西积分定理得