6.2.1　保角性

6.2.1　保角性

对于式(6.2.1)给出的分式线性映射,由于f′(z) = 因而f(z)在分母不为零的区域内是保角映射.

若对于式（6.2.1)给出的分式线性映射,当c 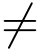0 时,规定当c = 0时,规定f(∞) = ∞,则分式线性映射将扩充z平面一一对应地映射为扩充w平面.下面我们说明分式线性映射在整个扩充复平面上都是保角的.

我们规定两条曲线在z = ∞处的夹角,等于它们通过变换w = z得到的象曲线在w =0处的夹角.

对于反演变换w =来说,因为 因而除去z = 0 与z = ∞,它是保角的.

在z = 0处,象点w = ∞,通过变换w* =将其变换到w* = 0 处看是否保角,由于得到w* =z,且

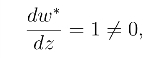
从而w =在z =0处是保角的.

在z =∞处,令z* = 则z =∞变为z* =0,由于则w =z*且

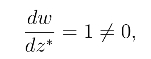
即w =在z =∞处也是保角的.

对于整线性映射w =az+b(a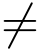0),由于

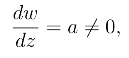
因而在z 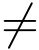∞时是保角的.在z =∞时,其象点w =∞,令则由w =az+b,得

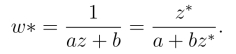
由(https://www.daowen.com)

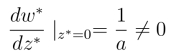
知,w =az+b在z =∞处也是保角的,因而w =az+b是扩充复平面上的保角映射.

我们可以把一个一般形式的分式线性映射分解成一些简单映射的复合.

当c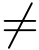0时,式(6.2.1)可写成

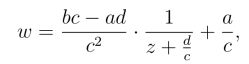
即

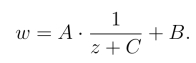
当c=0时,式(6.2.1)可写成

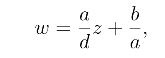
即

由此可见,一个一般形式的分式线性映射是由下列三种特殊映射复合而成：

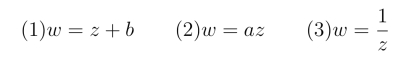
因此,我们有下面的定理

定理1 分式线性映射在扩充复平面上是一一对应的,且具有保角性.