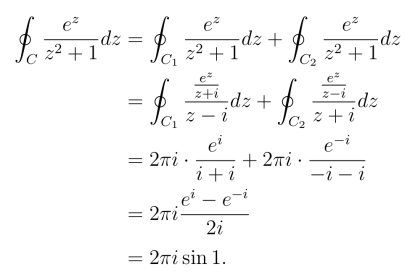3.4.1 柯西积分公式
设D为一单连通域,z0为D中的一点.若f(z)在D内解析,那么函数
在z0点不解析.下面考虑D内围绕z0的简单闭曲线C上积分
的计算.根据闭路变形原理,该积分值等于沿任何一条围绕z0的简单闭曲线上的积分.既然沿围绕z0的任何简单闭曲线积分值都相同.那么我们就取以z0为中心,半径为δ的圆周|z-z0| = δ(取其正向)作为积分曲线C.由于f(z)的连续性,在C上的函数f(z)的值将随着δ的缩小而逐渐接近于它在圆心z0处的值,从而使我们猜想积分
的值也将随着δ 的缩小而逐渐接近于
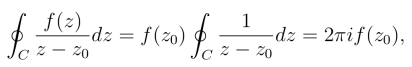
即
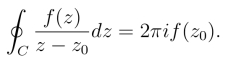
我们有下面的定理：
定理1(柯西积分公式) 若f(z)在区域D内处处解析,C为D内的任何一条正向简单闭曲线,它的内部完全含于D,z0为C内的任一点,那么
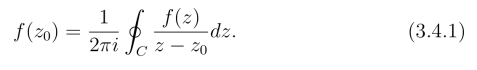
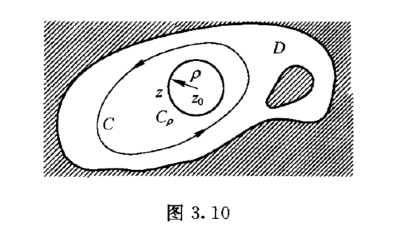
证明 取ρ充分小,在D内作正向圆周Cρ : |z -z0| = ρ,使Cρ及内部完全位于D内(图3.10),由于f(z)在z0连续,任意给定ε ＞0,存在δ ＞0,当|z-z0|＜δ时,有
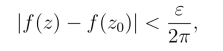
于是由式(3.1.4)和积分的估值定理得
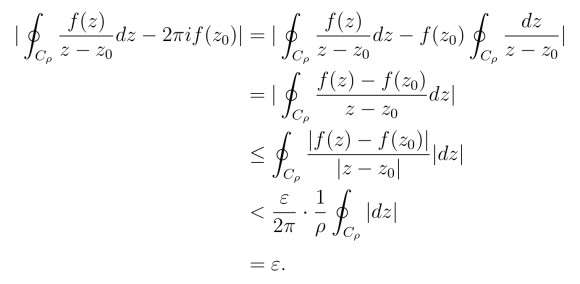
从而有
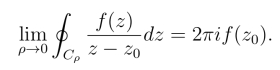
根据闭路变形原理,该积分值与ρ无关,从而有
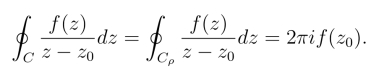
在定理1中,区域D是单连通域或多连通域均可,但积分曲线C及内部必须完全位于D内,因此该定理也可叙述为：
若f(z)在简单闭曲线所围成的区域内及C上解析,那么柯西积分公式(3.4.1)仍然成立.
公式(3.4.1)把一个函数在曲线C内部任一点的值用它在边界上的值来表示.也就是说若f(z)在区域边界上的值一经确定,那么它在区域内部任一点处的值也就确定.这是解析函数的又一特征.柯西积分公式不但提供了计算某些复变函数沿闭路积分的一种方法,而且给出了解析函数的一个积分表达式,是研究某些解析函数的有力工具.
若C是圆周z =z0+Reiθ,那么式(3.4.1)成为
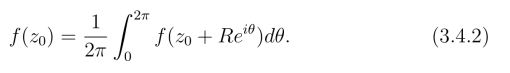
这就是说,一个解析函数在圆心处的值等于它在圆周上的平均值.
例1 计算积分
其中C 为正向圆周|z|=4.
解 根据柯西积分公式,得
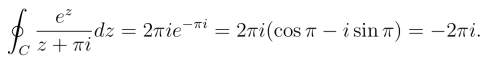
例2 计算积分
其中C为正向圆周|z|=3.
解 如图3.11所示,分别以z =i和z =-i 为圆心作两个小圆周C1和C2,
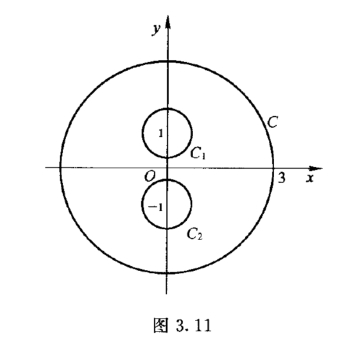
则
