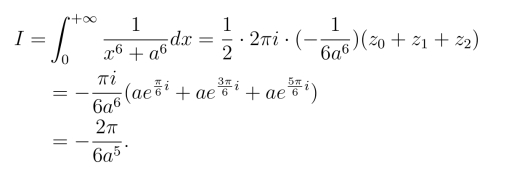5.3.2　形如的积分

5.3.2　形如 的积分

定理2 设f(z)在实轴上解析,在上半平面Imz ＞0除有限个奇点z1,z2,··· ,zn 外解析.若存在正数r,M 和α ＞1,使当|z| ≥r 且Imz ≥0 时f(z)解析且满足|f(z)|≤M/|z|α,则积分I2 =存在且有

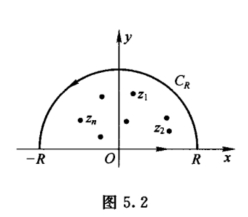
证明设CR为上半圆周z = Reiθ(0 ≤θ ≤π),取充分大的R 使R ≥r并且奇点z1,z2,··· ,zn均在由CR及实轴上从-R 到R 的一段所围成的闭路内(如图5.2),由留数定理得

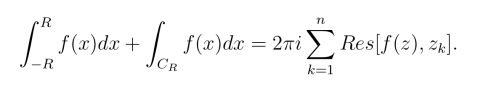
由于在CR上|f(z)|≤ 因此

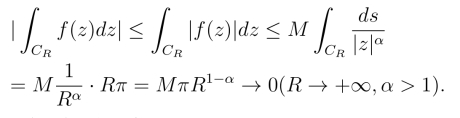
从而当R →+∞时可得所证结果

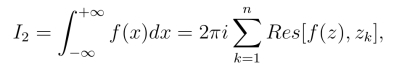
若f(x)=为有理函数,Q(x)在x轴上无零点,且Q(x)的次数至少比P(x)的次数高两次,则有

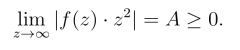
当|z|充分大时,有

即

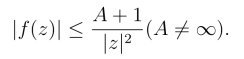(https://www.daowen.com)

于是由定理2可得:

推论 若f(x) =为有理函数,在上半平面上的奇点为z1,z2,··· ,zn,Q(z) 在实轴上无零点,且Q(z)的次数至少比P(z)的次数高两次,则式(5.3.2)成立.

例3 计算积分

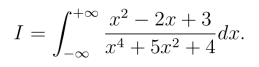
解 f(z)满足定理2推论的条件,在上半平面内只有两个简单极点z = i和z =2i,且

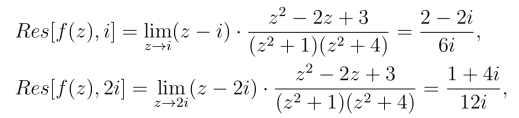
因此得

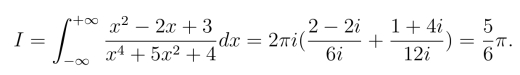
例4 计算积分

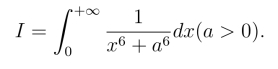
解 由于f(x)=为偶函数,因此

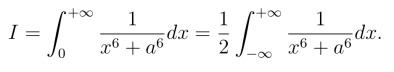
f(z)在上半平面有3个简单极点

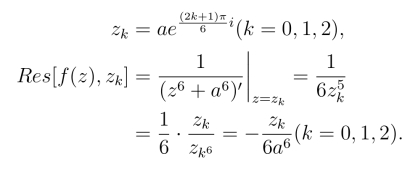
由定理2推论