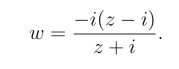6.2.3 保交比性
2026年01月14日
6.2.3 保交比性
定义1 由扩充复平面上4个有序的相异点z1,z2,z3,z4构成的比式
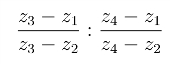
称为它们的交比,记作(z1,z2,z3,z4).
若4点中有一个为∞,应将包含此点的分子或分母用1代替,例如z1 =∞,则
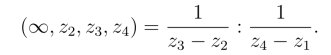
对于扩充z平面上4个有序的相异点z1,z2,z3,z4经整线性映射w =az+b,得到扩充w平面上的4个点w1,w2,w3,w4,由于
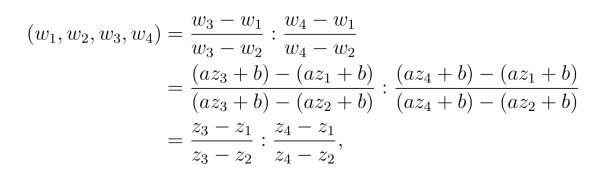
即整线性映射具有交比不变性.同样可验证w =![]() 具有交比不变性.
具有交比不变性.
综上可知,分式线性映射具有保交比性.
分式线性映射w =![]() 形式上有4 个常数,但实际上只有3个独立常数.
形式上有4 个常数,但实际上只有3个独立常数.
定理3 扩充平面的3个点z1,z2,z3在分式线性映射下,分别映射为扩充w平面的3个点w1,w2,w3,则此分式线性映射为
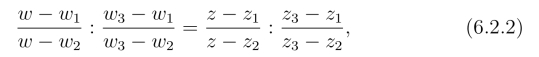
即(https://www.daowen.com)
![]()
证明易见式(6.2.2)确定了一个分式线性映射,使z1,z2,z3分别变为w1,w2,w3.
反过来,所求的分式线性映射存在,由于其保持交比不变,即得式(6.2.2).
推论(边界对应原理) 若分式线性映射将圆周C上的3 个点z1,z2,z3分别变为圆周Γ上的3个点w1,w2,w3,则该分式线性映射将C映射为Γ.
例1 求分式线性映射,使单位圆周|z| = 1 上的3个点i,-i,1分别对应0,∞,-1.
解 由定理2得此分式线性映射为
![]()
即
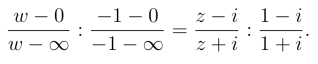
由
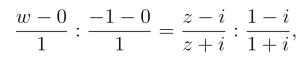
得到所求的分式线性映射为