6.2.4　保对称性

下面我们定义关于一个已知圆周的一对对称点.设C为以原点为中心,R为半径的圆周.在以圆心为起点的一条射线上,若有两点P 与P′满足关系式

OP ·OP′ =R2,

则称这两点为关于该圆周的对称点.

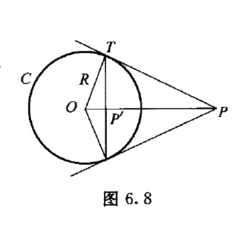
设P在C外,从P作圆周C的切线PT,由T作OP的垂直线TP′与OP并于P′,那么P与P′即互为对称点(图6.8).这是由于△OP′T ～△OTP.因此,OP′ :OT =OT :OP,即OP ·OP′ =OT2 =R2.

在扩充复平面上,规定无穷远点的对称点是圆心O.

关于直线的对称点,例如x轴,点z的对称点是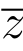,其余类推.

分式线性映射具有保持对称性不变的性质,简称保对称性.

定理4 设点z1,z2是关于圆周C的一对对称点,那么在分式线性映射下,它们的象点w1 与w2也是关于C的象曲线Γ的一对对称点.

证明从略.