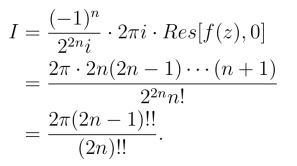5.3.1　形如的积分

5.3.1　形如 的积分

对于积分 若令φ= 则有

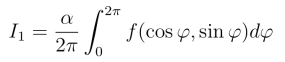
其中φ可看作圆周|z|=1的参数方程的参数.于是令z =eiφ(0 ≤φ ≤2π),则有dz =izdφ,且有

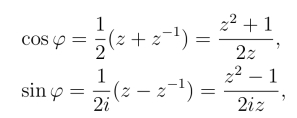
当φ从0变到2π时,沿z圆周|z|=1正向绕行一周,于是有

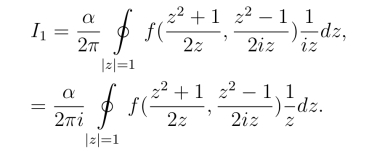
若函数F(z) = 在|z| ＜1内只有有限个奇点z1,z2,··· ,zn,则由留数定理得

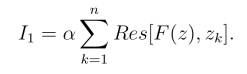
于是有下面的定理:

定理1 设I1 = 若函数F(z) = 在|z|=1 圆周上解析,在|z|＜1 内除有限个奇点z1,z2,··· ,zn外解析,则有

实际计算中,只要令

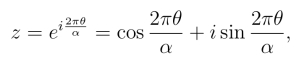
就可将定积分I1变为沿单位圆周|z|=1的复积分,然后再利用留数定理进行计算.

特别地,当α=2π时,

例1 计算积分

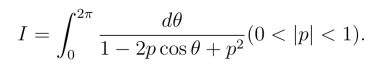
解 令z =eiθ,则

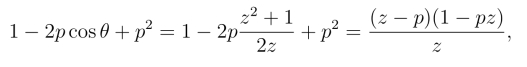(https://www.daowen.com)

从而有

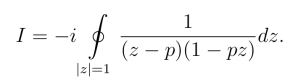
函数f(z) =在|z| ＜1内只有一个简单奇点z = p,在|z| =1上无奇点,且

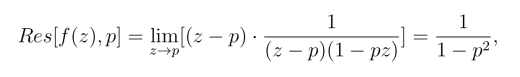
由留数定理得

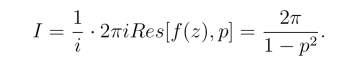
例2 计算积分

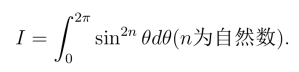
解 由于sin2n x以π为周期,因此

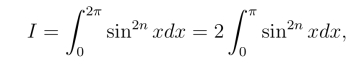
令z =则

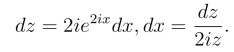
由于

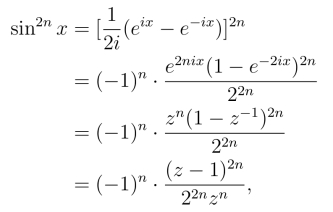
从而有

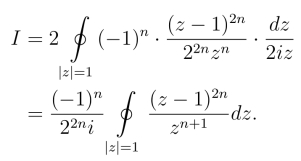
由于函数f(z)= 在|z|=1的内部只有一个n+1级极点z =0,在|z|=1上无奇点,而

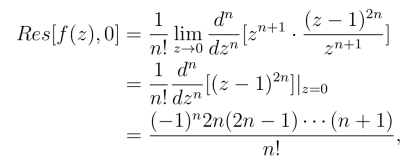
由留数定理得