3.2.2 柯西-古萨基本定理
在柯西积分定理中要求曲线C是简单闭曲线.事实上,对任何闭曲线该结论成立,这就是柯西- 古萨(Cauchy-Goursat)基本定理.
定理2(柯西-古萨基本定理) 若函数f(z) 在单连通域D内解析,则对D内的任何闭曲线C有
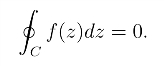
对于非简单闭曲线,可看作是由多个简单闭曲线组成(图3.4),则由柯西积分定理可直接得到定理2.
由该定理可以得到下面推论.
推论若函数f(z)在单连通区域D内解析,则它在D内从定点z1到动点z2的积分值与D内所取路径无关.
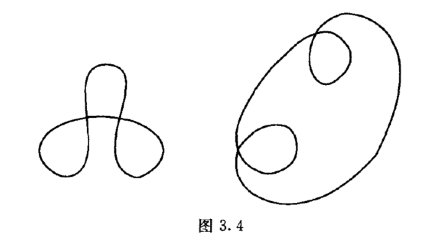
证明 设C1和C2为z1到z2的任意两条曲线,则C1 + C-2 为一有向闭曲线(图3.5),由定理2得
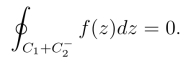
又由于
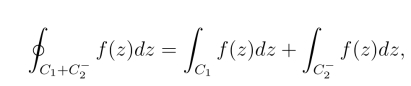
从而
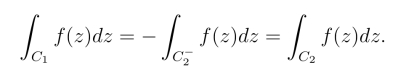
由于积分只与z1,z2有关,不依赖于D内连接z1到z2的曲线,这时可将积分记作
