参考答案

参考答案

习题一

1.B;2.D;3.A;4.D;5.B;6.D;7.A;8.B;9.A;10.A;

11.以i为顶点，与正实轴成角度的角形域的内部;

12.+kπ,k =0,±1,±2,±3,...;

13.4n-1

14.

15.z =

18.n=4k,k =0,±1,±2,±3,...

19.(1)一个点;(3)双曲线y =在第一象限的一支;(4)直线y =3;

21.提示：利用三角形三顶点都在圆上.

22.提示：利用圆周的一般方程.

习题二

1.B; 2.C; 3.D; 4.C; 5.C;

6.2kπ+,k =0,±1,±2,···

7.±i

8.1,-3,-3

9.零与负实轴

10.2sinzcosz

11.f′(z)=-i

12.ln5-iarcctan+(2k+1)πi,k =0,±1,±2,···

13.

14.抛物线：v2 =-4(u-1),0 ≤u ≤1

15.(1)圆：;(2)圆：;(3)直线：v =-u;(4)直线：

16.(1)w1 =-i,w2 =-2+2i,w3 =8i;(2)0 ＜argw ＜π

17.(1)在Rez =可导，处处不解析;(2)在C处处可导、处处解析;

(3)在C\{-1,1}上处处可导、处处解析;(4)在C上处处可导、处处解析.

18.极点：-2、-2、-1、1

19.(1)在C上解析,f′(z) = cosz +3i; (2)在上解析,f′(z) = (3) 只在0 处可导,导数为0,处处不解析; (4) 只在-i处可导,导数为-2,处处不解析;(5)在直线y =x上可导,导数为2x(1-i),在C上处处不解析.

20.提示：用C-R条件

23.(1)-ei;(2);(3)sin1cosh1+icos1sinh1;(4)0,±1,±2,···;(5)ln5+iarctan0,±1,±2,···.24.(1)(2k+1)πi,k =0,±1,±2,···;(2)(k-)π,k =0,±1,±2,···;(3)i;(4)kπi,k =0,±1,±2,···.

习题三

1.(1)4πi;(2)8πi.

2.(1)1;(2)2;(3)2.

3.

4.

7.不一定，如f(z)=沿圆周|z|=1 的积分为0,而z0 =0在|z|=1 的内部.

8.被积函数在|z|≤1上解析

9.当r ＞|z0|时，2πi;r ＜|z0|,其积分值为零

10.被积函数在1 ≤|z|≤2上解析

11.(1)2πi; (2)4πi; (3)0; (4)4πi; (5)-2πi

13.e-1-1

14.(1)- (2)i sinh 1; (3)-2; (4)π- 从所给起点到终点的积分路径在整个复平面都是任意的

15.0

16.提示：考虑被积函数的奇点和原函数，这两个原函数在右半平面上解析,该平面是为单连通域,

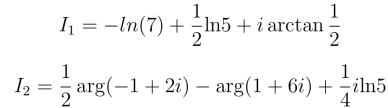
17.(1)

18.z0在C1内部，I =z20; (2)z0在C2内部，I =sin z0;I =0,其他

19.0,当|α|＞1;πeαi,当|α|＜1

25.(1)f(z) = z3 +i; (2)f(z) = z2; (3)f(z) = zez; (4)f(z) = (1-i)z3;(5)f(z)=

26.不一定.

27.提示：用3.5节定理1和C-R方程，以及拉普拉斯方程。

习题四

1.由定理1或2，其结论显然成立.

2.如调和级数

3.(1) i (2) |zn|→0 (3)zn →∞,发散 (4)发散

4.(1) 通项的模|αn|→1(n →∞),发散(2) 绝对收敛(3) 发散(4) 绝对收敛

5.不能

6.和函数在收敛圆域|z-z0|＜R内解析，其积分与路径无关.当积分下限是该圆内其他某一定点z1 时,该式的右端还需减去常数c=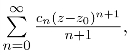 很麻烦.

7.(1)z0 = 0,R = 1;(2)z0 = -i,R = 2;(3)z0 = i,R =;(4)z0 = 0,R =1;(5)z0 =-2i,R=∞;(6)z0 =0,R=1.

8.提示：用定理2或定理3.

9.f(z)的奇点为z =1和2,z0 =i到奇点的最短距离为R=|i-1|=

10.f(z)的泰勒级数展开式是对应复变函数f(z)只在实轴上取值的特殊情形，而z =±i为f(z)的奇点,由本节定理,f(z) 在z0 =0 的泰勒级数的收敛半径R=1.

11.同本节例6.

12.

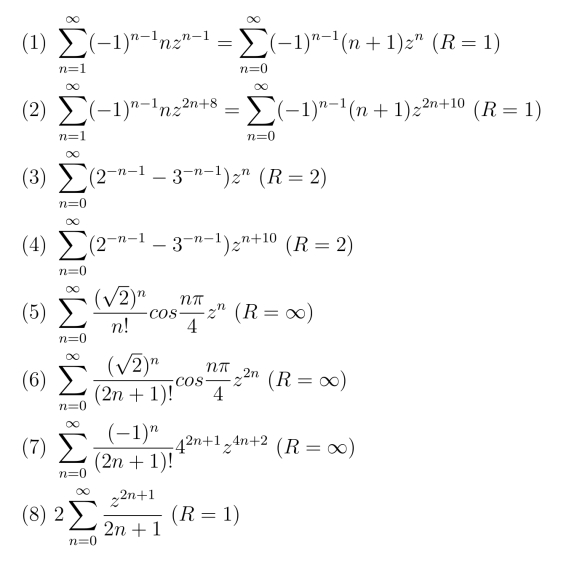
13.

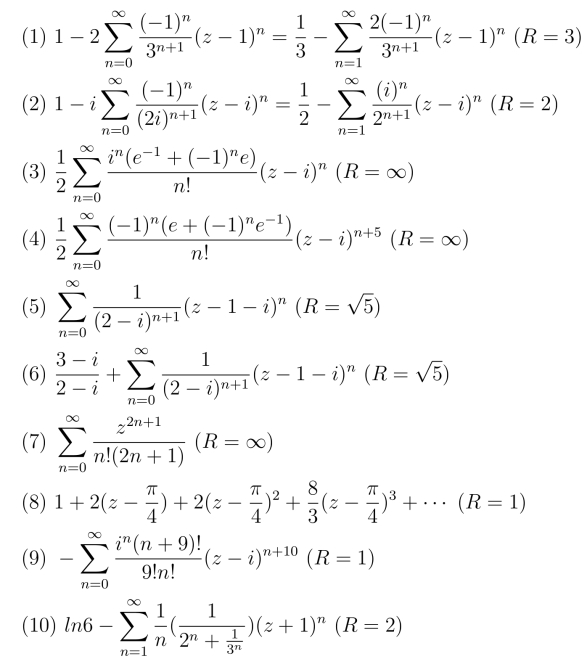
14.不矛盾,f(z)的洛朗级数展开式的惟一性是对给定的某个环域而言,其条件是f(z)在该环域内解析.

15.环域有0 ＜|z-i|＜1,1 ＜|z-i|＜2,2 ＜|z-i|＜3,3 ＜|z-i|＜∞

16.

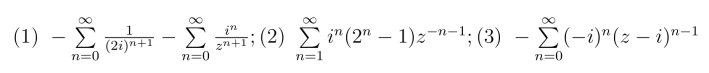
17.(1) 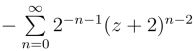;(2)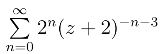

18.所给每个函数都在环域0 ＜|z| ＜∞内解析，该环域既是点z0 = 0的去心邻域,又是点∞的邻域.

19.

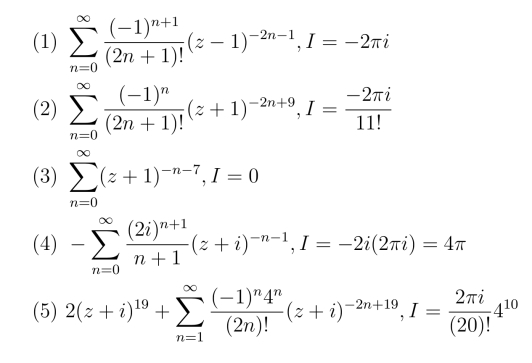
20.(1)收敛;极限为0; (2)发散; (3)收敛，极限为0.

21.(1)原级数收敛，但非绝对收敛; (2)原级数收敛，但非绝对收敛;(3)原级数收敛，且为绝对收敛; (4)原级数发散.

22.(1)不正确.幂级数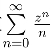收敛圆为|z| = 1,当z = -1时,级数收敛,当z =1时,级数发散.

(2)不正确.根据幂级数的性质，其在收敛圆内不可能有奇点.

(3)不正确.f(z)=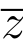在z0连续,但不解析,不能在z0点展开成泰勒级数.

23.(1)(2)2(4)∞

24.收敛半径R=1,收敛圆|z-3|=1,利用

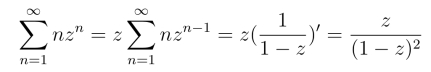
有

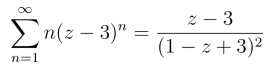
和函数

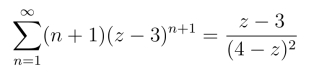
25.提示：|(Recn)zn|＜|cn||z|n

28.f(z)=z|＜∞,c 为任意常数.

29.f(z)=(-1)n(n+1)zn,|z|＜1.

30. 奇点为z = 0 与zk =,(k = 0,±1,±2,···),当k →∞时,zk →0.因此不存在一个去心领域0 ＜|z| ＜k 使得在其内解析,所以不可能在0 ＜|z|＜R 内把tan1 z 展开成洛朗级数.

31.2πi

习题五

1.(1) z =0,一级极点; z =±i,二级极点;

(2) zk =kπ(k =0,±1,±2,···),一级极点;

(3) z =0,二级极点; zk =2kπi(k =±1,±2,···),一级极点;

(4) z =0,可去奇点;

(5) z =±i,二级极点; zk =(2k+1)πi(k =1,±2,···),一级极点;

(6) zk =(k =0,1,2,···n-1),一级极点;

z =±i,二级极点;

(7) z =1,二级极点; z =-1,一级极点;

(8) z =1,本性奇点;

(9) z =0,二级极点; 一级极点

3.(1) 当m 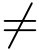n时,z0为极点,级为max(m,n); 当m = n时,z0 为极点,它的级≤m,也可能是可去奇点;

(2) z0为m+n级极点;

(3) 当m 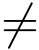n时,若m ＞n,则z0为m-n级极点; 若m ＜n,当定义 = 0时,z0为n-m级零点.当m=n时,z0 为可去奇点

4.不对.因为f(z)在z = 1处的去心邻域应为0 ＜|z-1| ＜1,应在此邻域内将f(z) 展成洛朗级数.

5.(1) z =0,三级极点; z =∞,可去奇点

(2) z =0,可去奇点; z =∞,本性奇点

(3) z =1,二级极点; z =∞,三级极点

6.(1) Res[f(z),0]=0

(2) Res[f(z),0]=

(3) Res[f(z),1]=

(4) Res[f(z),kπ+,(k =0,±1,±2,···)

(5) Res[f(z),0]=0;Res[f(z),kπ]=(-1)k(),(k =±1,±2,···)

(6) Res[f(z),0]=

(7) Res[f(z),1]=0

(8) Res[f(z),i]=

(9)当n为奇数时,Res[f(z),0]=0; 当n=2k为偶数时,Res[f(z),0]=

7.(1) 0 (2) 2πi (3) 4πi (4) 4πe2i (5) -4πi(6) 当m ≥3且为奇数时,积分等于(-1) 当m 为其他整数时,积分等于0

8.(1) -sinh 1 (2) 0

9.(1) 2πi (2) (3) 当n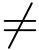1 时,积分等于0; 当n=1 时,积分等于2πi

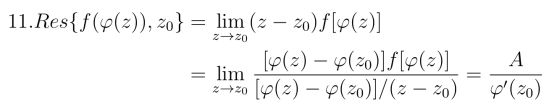
12.

13.

14.

15.(1); (2) ; (3); (4) πe-1 cos 2; (5)

17.(1) 2πi;(2) 2πi ;(3) 0.(https://www.daowen.com)

18.4个

22.(1) z =0,一级极点,z =±i,三级极点;

(2) z =0,可去奇点;

(3) z =1,本性奇点;

(4) z =±i,二级极点,zk =(2k+1)i(k =1,±2,···),一级极点;

(5) z =0,三级极点,zk =2kπi(k =±1,±2,···),一级极点;

(6) z =0,二级极点,均为一级极点.

23.(1)Res[f(z),0]=

(2) Res[f(z),0]=0

(3)Res[f(z),0]=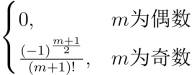

24.(1) Res[f(z),1]=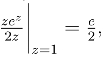

Res[f(z),-1]=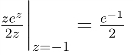

Res[f(z),∞]=-{Res[f(z),-1]+Res[f(z),1]}==-cosh 1

(2) Res[f(z),∞]=

25.Res[f(z),2]+=-Res[f(z),∞]=1

26.(1)

(2)

(3) 当m ＞2且为偶数时,积分等于零; 当m ＞2且为奇数时,积分等于(-1)

27.(1) 2πi(2)

28.πe-2(cos 2+i sin 2) 29.

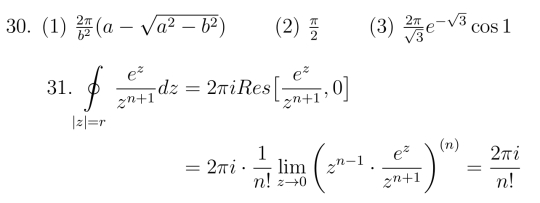
在C :|z|=r上,令z =reiθ,由

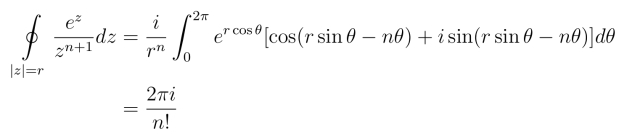
可证得.

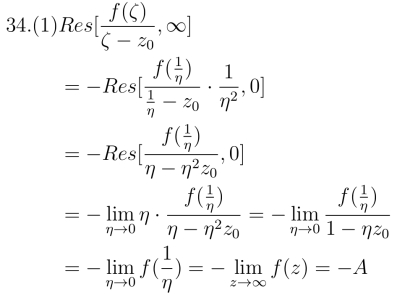
从而(1)z0 ∈D,则

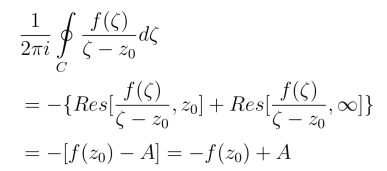
(2) z0 /∈D,则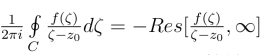=-(-A)=A

35.提示: 令f(z)=(z-z0)nφ(z),计算被积函数在z0点处的留数.

36.提示: 令f(z)=计算被积函数在z0 点处的留数.

37.因为a是f(z)的n级极点,所以f(z) =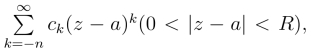于是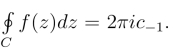又由于g(z) = (z-a)nf(z) = 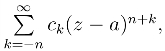因此g(n-1)(a)=(n-1)!c-1,c-1 = 即

习题六

1.(1)伸缩率2，转动角π/2; (2)伸缩率1，转动角π; (3)伸缩率e,转动角1.

2.Γ1 :Reω =3;Γ2 :Imω =4

3.转动角设z = x+iy，伸缩率|f′(z)| =当|f′(z)| ＜1，即(x+1)2 +y2 ＜时缩小，反之放大.所以，在以z = -1 为中心，半径为的圆内缩小，圆外放大.

4.(1)|ω-1|＞1,Reω ＞0 (2)|ω-i/2|＜1/2,Reω ＞0

5.ω =i/z;|ω|＞1

6.ω =ela(z-z0)/(z+z0)(Rez0 ＞0,0 ≤a ＜2π)

7.(1)ω =i(2z-1)/(z-2) (2)ω =i(2z-1)/(z-2) (3)ω =(z-i)/(z+i)(4)ω =-i(z-i)/(z+i) (5)ω =-(z+1)/(2z)

8.略

9.所给区域可表示为2a ＜Argz ＜2a+2π,ω = 的单值解析分支为ω1 =e-2laz和ω2 =e[ln(-ω1)+πl]/2与ω =elaω2 的复合映射ω =e[ln|z|+lArgz]/2

10.ω =

11.ω =

12.ω = (h为任意正实数)

13.ω =H[ln(eπz/H -eπa/H)]/π

14*.提示ω = coshz可分解为ω1 = ez和ω = (ω1+1/ω1)/2的复合映射；ω =sinhz 可分解为ω1 =iez和ω =-i(ω1+1/ω1)/2的复合映射.

(1)Imω ＞0(2)Imω ＜0(3)Imω ＜0

(4)Imω ＞0(5)Reω ＞0(6)Reω ＜0

(7)Imω ＜0(8)Imω ＞0

15.ω =2z3/2

16.ω =2z(z+1+lnz)

17.ω =

18.

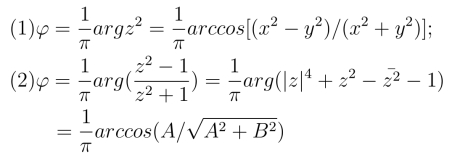
其中A=(x2+y2)2-1,B =4xy

19.伸缩率：|ω′(i)|=2；转动角：Argω′(i)=ω平面上虚轴的正向.

20.在导数不等于零的条件下具有伸缩率和旋转角的不变性；映射ω =z2在z =0 处不具有伸缩率和旋转角的不变性.

21.略22.略23.略24.略

25.(1)ω =

(2)ω =

(3)ω =

26.(1)ω

(2)ω =

(3)ω =

(4)

27.把单位圆|z|＜1映射成ω平面上的下半平面：

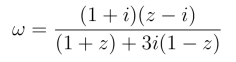
28.ω =其中Rea ＞0,θ为任意实数.

29.ω =

30.z =coshω

习题七

1.D2.D3.D4.A5.B6.C7.B8.A9.D

10.B

11.

12.

13.e-atμ(t)

14.f(t)=

15.

16.

17.eiω+2πδ(ω+1)

18.

19.2πδ(ω)

20.

21.e-t =

22.g(ω)=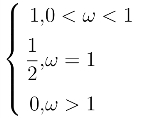

23.略

24.

25.f(t)=

26.

27.f(t)=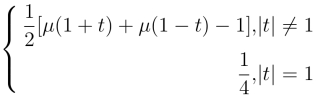

28.(1)e-ieω

29.F(ω)=

30.-F(ω)-ωF′(ω)

31.

32.

33.略34.略

习题八

1.B 2.A 3.C 4.A 5.C 6.B 7.D 8.A 9.B 10.D

11.

12.

13.cos 3t+

14.

15.

16.tet

17.

18.-F′′′(p-5)

19.

20.

21.

22.(4)

23.(1)(4)

24.(1)eu(t-5) (2)(1+t+t2)u(t-1) (3)2u(t-1)-u(t-2)

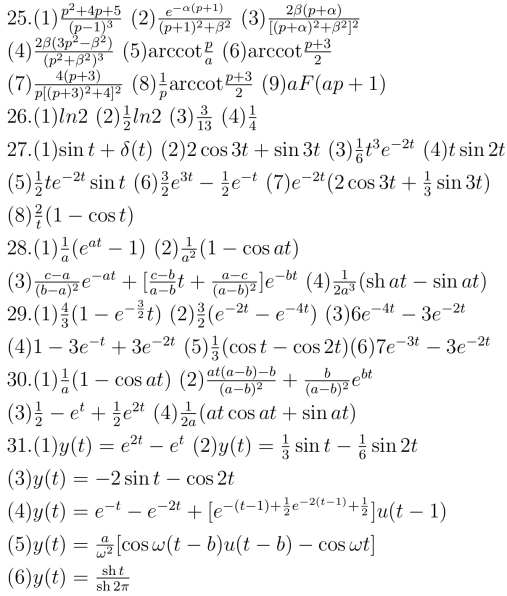
32.(1)

(2)

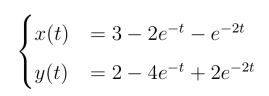
(3)

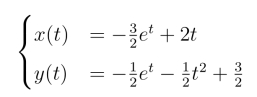
33.(1)y(t)=(1-t)e-t

(2)y(t)=sin t

(3)y(t)=sin t

(4)y(t)=a(t+

34.略

35.略

习题九

1.略

2.略

3.略

4.略