5.5 小结
在本章中,我们首先对解析函数的孤立奇点进行了分类.
设z0为解析函数f(z)的孤立奇点,若f(z)在以z0为中心的洛朗展开式
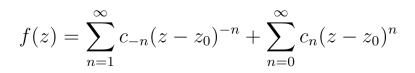
中,不含、只含有限个、含无数多个z-z0的负幂项,则称z0分别为f(z) 的可去奇点、极点、本性奇点,给出了z0 为f(z)的可去奇点、极点、本性奇点的充要条件分别为当z →z0 时,f(z) 的极限为有限数、为无穷大、不存在且不为无穷大.
称R ＜|z| ＜+∞为无穷远点z →∞的去心邻域,特别地当R = 0 时,邻域R ＜|z| ＜+∞既是z →∞的去心邻域又是z = 0的去心邻域.若函数f(z)在z = ∞的某个去心邻域内解析,则称z = ∞为f(z) 的孤立奇点.函数f(z) 在z = ∞的性态是由
在ζ = 0 处的性态定义的,即若ζ = 0为
的可去奇点、极点、本性奇点,则z = ∞为f(z)的可去奇点、极点、本性奇点.
关于极点,我们有如下形式的等价定义.
若函数f(z)可表示成
其中φ(z)在z0点解析,并且φ(z0)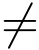
0,则称z0为f(z) 为m级极点.
为判断极点的级,我们引入解析函数零点的概念.
若函数f(z)能表示成
其中ψ(z)在z0点解析,并且ψ(z0)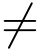
0,则称z0为f(z)的m级零点.给出了z0为f(z)的m级零点的充要条件为
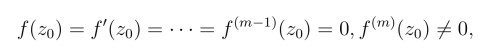
证明了z0为f(z)的m级零点的充要条件为z0是
的m级极点.
本章的中心问题是留数和留数定理.在有限点和无穷远点的留数的定义不相同.
设z0为f(z)的孤立奇点,则f(z)在z0的留数
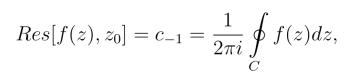
其中C为去心邻域0 ＜|z-z0|＜R内的任意一条正向简单闭曲线,c-1为f(z)在该去心邻域内的洛朗展开(z-z0)-1的系数.
如果z =∞为f(z)的孤立奇点,那么f(z)在z =∞的留数
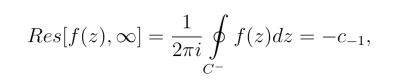
其中C为R ＜|z| ＜+∞内绕原点的任意一条正向简单闭曲线,c-1为f(z)在z = ∞的去心邻域内的洛朗展开式中z-1 的系数,要特别注意的是在z = ∞的去心邻域内的洛朗级数是被看作以原点为中心的圆环域展开的,即z0 =0.
留数定理 若函数f(z)在简单闭曲线C 上处处解析,在C的内部除有限个孤立奇点z1,z2,··· ,zn外解析,则有
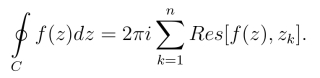
这个定理把求沿封闭曲线C的积分,转化为求被积函数在C中的各孤立奇点处的留数.
从闭路变形原理可以直观地看出留数定理的正确性,如下图所示.
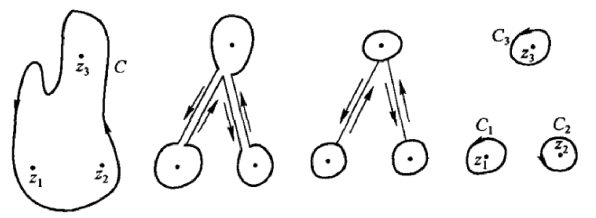
关于留数的计算,应根据奇点的类型选用不同的方法,当z0为f(z)的可去奇点时,则Res[f(z),z0] = 0; 当z0为f(z) 的本性奇点时,一般通过将f(z)展开成洛朗级数的方法求留数,当z0为f(z)的极点时,可用下面的规则计算留数.
规则1° 若z0为f(z)的一级极点,则有
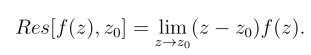
规则2° 若z0为f(z)的m级极点,则有
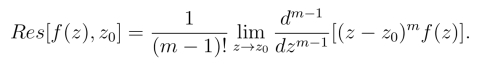
规则3° 设f(z)=P(z)/Q(z),其中P(z)和Q(z)在点z0 都解析,若P(z0)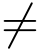
0,Q(z0)=0且Q′(z0)
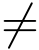0,则z0为f(z)的一级极点,且有
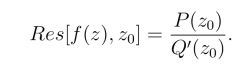
但是当z0为f(z)的m级极点,而m较大时,由于求导次数太多,使得计算复杂,也可通过将f(z) 展开成洛朗级数的方法求留数.
关于无穷远点的留数,应特别注意的是,当z =∞为f(z)的可去奇点时,留数不一定等于零,例如z =∞是f(z)=
的可去奇点,但由于c-1 =-1,所以Res[f(z),∞]=1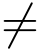
0,这与有限点的留数的情况不同.
关于无穷远点的留数的计算,可以通过将函数f(z)在z =∞的去心邻域内展开成洛朗级数的方法求留数,也可以通过下面的定理计算留数.
定理1 若函数f(z)在环域R ＜|z|＜∞内解析,则有
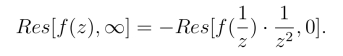
定理2 如果函数f(z)在扩充复平面上除孤立奇点zk(k =1,2,··· ,n)与∞外,处处解析,那么
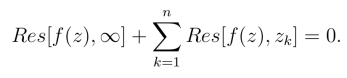
利用定理2,可以通过计算各有限远奇点处的留数来得出在∞点处的留数,也可以反过来用.
关于留数在定积分计算中的应用,我们介绍了三种不同类型的积分:
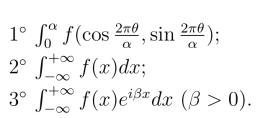
其基本思想是把所给定积分化为解析函数沿某条闭曲线的积分,然后利用留数定理来计算其积分值,这种方法通常称为围道积分法.
在本章的最后是对数留数和辐角原理,它们可帮助我们判断一个方程f(z)=0的各个根所在的范围.