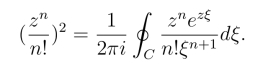3.4.2 高阶导数公式
解析函数不仅有一阶导数,而且有各高阶导数,它的值也可以用函数在边界上的值通过积分来表示.但是对于一元实函数来说,它在某一区间上可导,其导数在这区域上是否连续也不一定,更不要说它有高阶导数存在了.
关于解析函数的高阶导数我们有下面的定理.
定理2 解析函数f(z)的导数仍为解析函数,它的n阶导数为
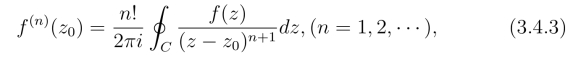
其中C为在函数f(z)的解析区域D内围绕z0 的任何一条正向简单闭曲线,而且它的内部全含于D.
证明 设z0为D内任意一点,先证n=1的情形,即
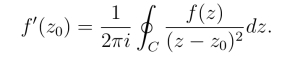
根据定义
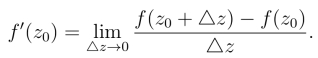
从柯西积分公式得
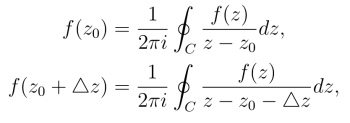
从而有
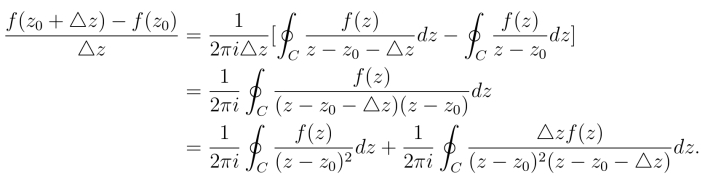
因为f(z)在C上是解析的,所以在C上连续,从而在C上是有界的.即存在一个正数M,使得在C上有|f(z)| ≤M.设d 为从z0到曲线C上各点的最短距离(图3.12),并取|△z|适当地小,使其满足
则有
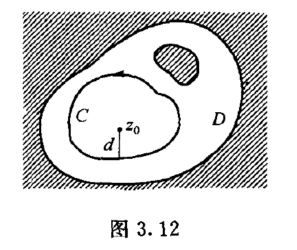
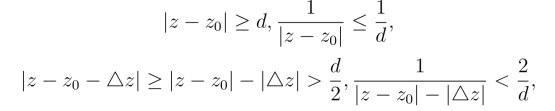
于是
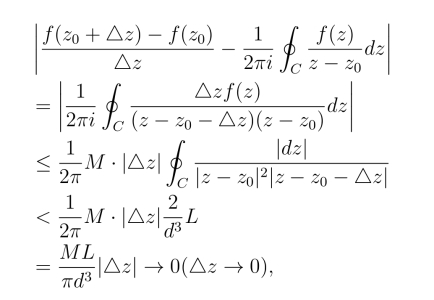
即
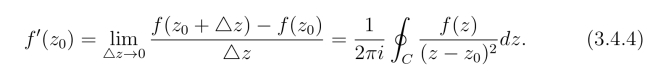
这表明了f(z)在z0的导数可以由把式(3.4.1)的右端在积分号下对z0求导而得.
假定当n=k(k ＞1)时公式成立,即有
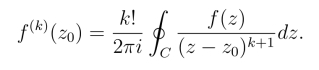
由此来推证当n=k+1时公式也成立.为此考察
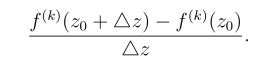
令△z →0,取极限,用类似于n=1情形的推证方法可以证明
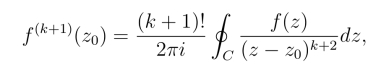
从而证明了当n为任何正整数时,公式
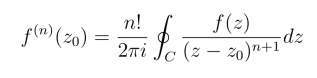
都成立.
根据解析函数的定义,由上述结论,易知解析函数f(z)的各阶导数f(n)(n=1,2,···)都是解析函数.
高阶导数公式的作用,不在于通过积分来求导,而在于通过求导来计算积分.
例3 计算积分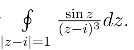
解 函数
在圆周|z-i|=1内的z =i处不解析,但sin z在|z-i|≤1上处处解析,因此
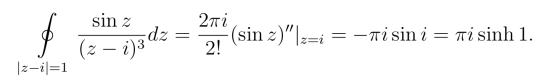
例4 计算积分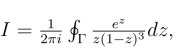
其中Γ为包含0,1的简单闭曲线.
解 在Γ的内部以原点为中心作一个正向圆周C0,以1为中心作一个正向圆周(图3.13),则被积函数在由C,C0和C1所围成的区域内是解析的,根据复合闭路定理有
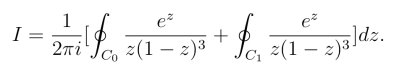
由于
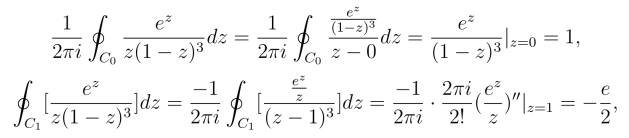
因此
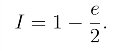
例5 试证
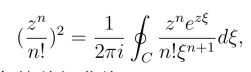
其中C是围绕原点的一条简单闭曲线.
证明 令f(ξ) = 
则因为f(ξ)在ξ 平面上解析,所以由高阶导数公式,有
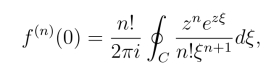
而
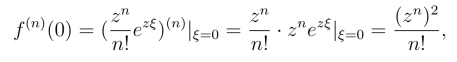
所以
