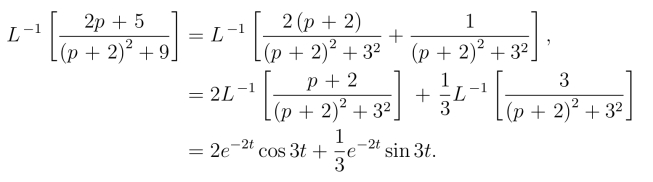8.2 拉氏变换的性质
这一节将介绍拉氏变换的几个基本性质,它们在拉氏变换的实际应用中都是很有用的.为了叙述方便,假定在这些性质中,凡是要取拉氏变换的函数都满足拉氏变换存在定理中的条件,并且把这些函数的增长指数统一地设为c.在证明这些性质时,不再重复这些条件.
1.线性性质
设α,β为常数,且
则有
或
2.相似性质
设a ＞0,若L[f(t)]=F (p),则
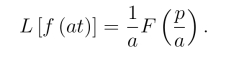
类似有
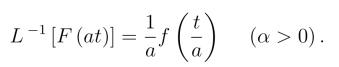
以上两条性质的证明与傅氏变换相应的性质的证明是一样的.
3.微分性质
设L[f(t)]=F (p),L[f′(t)]存在,则
证明
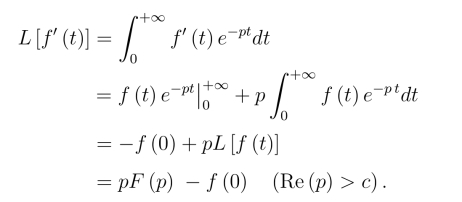
推论设
存在,则
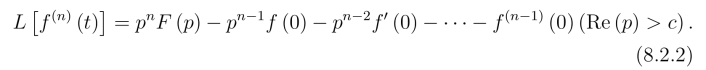
特别当f(0)=f′(0)=···=f(n-1)(0)=0 时,有
由拉氏变换存在定理的结论(8.1.2)式,可得如下象函数的微分性质,即
设L[f(t)]=F (p),则
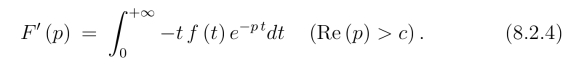
更一般有
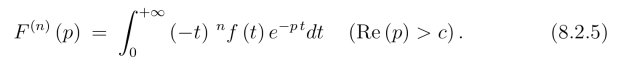
例1 利用线性性质求函数f(t)=ch(kt) 的拉氏变换.
解
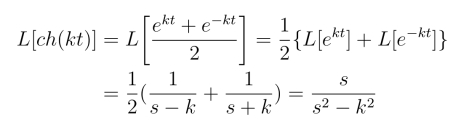
同理可得
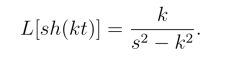
例2 求L[cos kt](其中k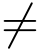 
0).
解 f(t)=cos kt,则
且f(0)=1,f′(0)=0.由微分性质,得
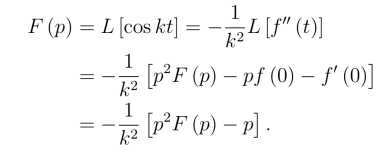
由此式可解出
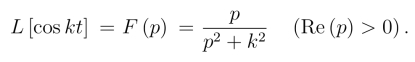
例3 利用微分性质求f(t)=tm的拉氏变换(m 为非负整数).
解 因为
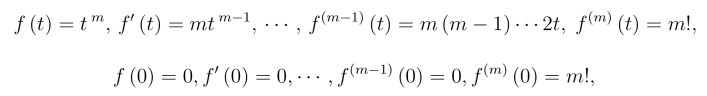
而
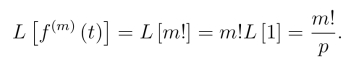
由拉氏变换微分性质(8.2.3),得
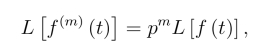
即
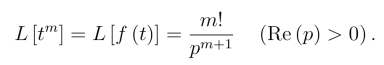
这个结果与§1例4的结果一致.
例4 求函数f(t)=t sin kt的拉氏变换.
解 因为L[sin kt]=
由象函数的微分性质可得
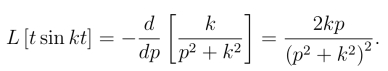
同理可得
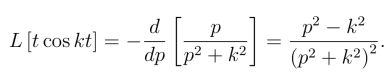
4.积分性质
若L[f(t)]=F (p),则
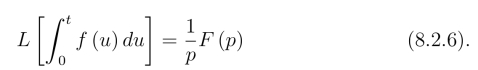
证明 设g(t)=
则有
且g(0)=0.由拉氏变换的微分性质(8.2.1)式
即
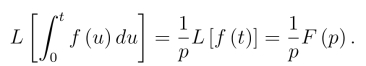
由拉氏逆变换存在定理,可以得到象函数的积分性质,
若L[f(t)]=F (p),则
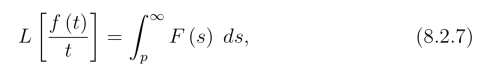
或
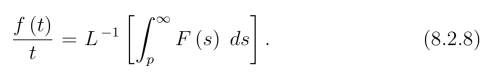
特别是当
存在时,在(8.2.7) 中,令p=0可得(https://www.daowen.com)
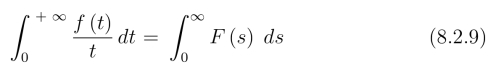
(8.2.9)给我们提供了一种求反常积分的办法.
例5 求
解 因为L[sin t]=
由象函数的积分性质(8.2.7),得
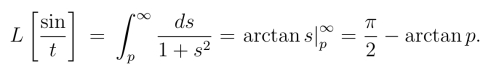
即
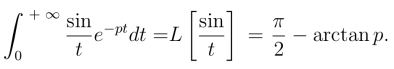
在上式中令p=0,得
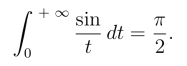
这个结果与第七章§1例1一致.
例6 求积分
解 由(8.2.9)
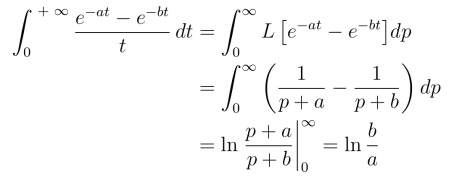
5.延迟性质
若L[f(t)]=F (p),又t ＜0时,f(t)=0,则对任一非负实数t0,有
或
证明 由拉氏变换定义
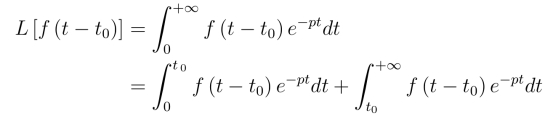
由t ＜0时f(t) = 0,得上式右端的第一个积分为零.对第二个积分,令u =t-t0,得
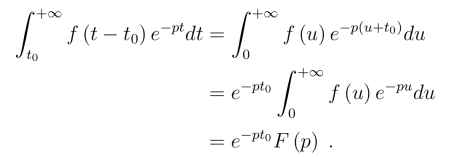
因此
延迟性质也称时移性质.f(t-t0) 与f(t)相比,f(t)是从t = 0开始有为非零数值,而f(t-t0)是从t = t0 开始才有为非零数值,即延迟了一个时间t0.如图8-1.
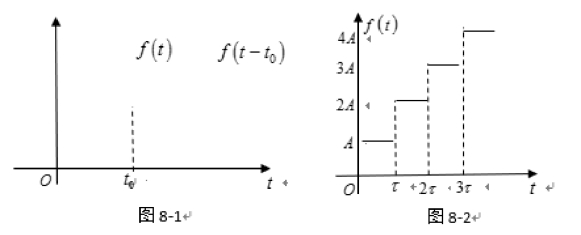
在本章第一节有过约定t ＜0时,f(t)=0,即f(t)应理解为f(t)u(t).这样延迟性质的公式(8.2.10)
应理解为
(8.2.11)式
应理解为
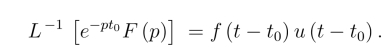
关于这个问题,我们还会在本章评注中通过例题进一步说明.
例7 求函数u(t-t0)=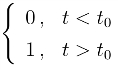
的拉氏变换.
解 因为
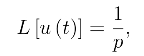
由延迟性质,得
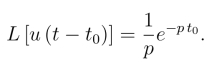
例8 求如图8-2所示的阶梯函数f(t)的拉氏变换.
解 利用单位阶跃函数,将f(t)表为
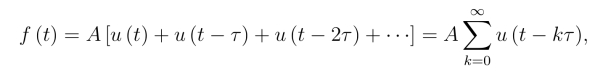
两边取拉氏变换,并假定右边的拉氏变换可以逐项进行.事实上,对满足拉氏变换存在定理条件的函数f(t)及τ ＞0,都有
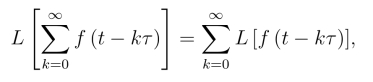
得
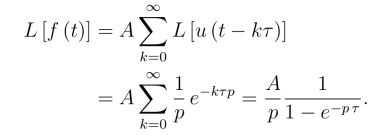
例9 求f(t)=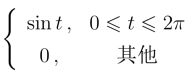
的拉氏变换.
解 因为f(t)可以改写为
而
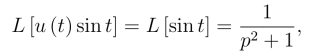
由线性性质及延迟性质,得
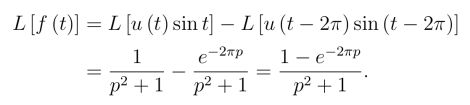
例10 设f(t)=(t-1)2,试求f(t)的拉氏变换.
解 因为f(t)=(t-1)2 =t2-2t+1,所以
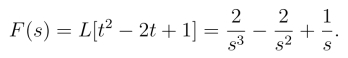
6.位移性质
若L[f(t)]=F (p),则有
证 由定义
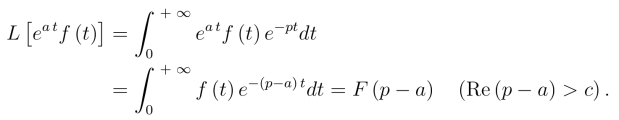
例11 求L[e-p0 t cos kt] 和L[e-p0 ttn].
解 由
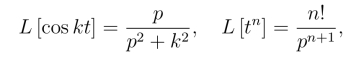
利用位移性质,得
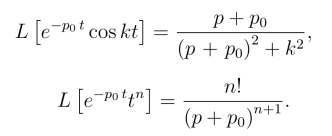
例12 求
解
