4.1.2　复数项级数的收敛性及其判别法

4.1.2　复数项级数的收敛性及其判别法

设{αn}={an+ibn}(n=1,2,···) 为一复数列,表达式

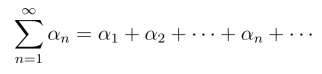
称为无穷级数,其前n项的和

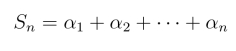
称为级数的部分和.

若该部分和数列收敛,其极限为S,则称上述复数项级数收敛,且称S 为该级数的和,记为

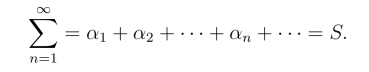
若部分和数列{Sn}发散,则称级数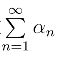发散.

定理4 级数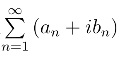 收敛的充要条件是其实部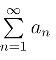级数和虚部级数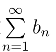都收敛.

证明 因

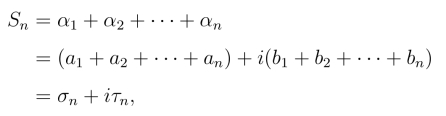
其中σn =a1+a2+···+an,τn =b1+b2+···+bn 分别为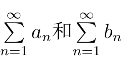 的部分和.由定理2,Sn 有极限存在的充要条件是σn 和τn 的极限存在,即级数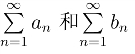都收敛.

定理4将复数项级数的审敛问题转化为实数项级数的审敛问题,而由实数项级数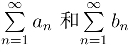 收敛的必要条件

(https://www.daowen.com)

立即可得

定理5 复数项级数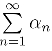收敛的必要条件是

如果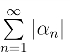收敛,那么称级数 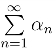为绝对收敛.非绝对收敛的收敛级数称为条件收敛级数.

定理6 若也收敛.

证明 由于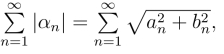而

根据实数项级数的比较准则,可知级数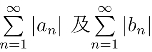都收敛,因而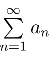和也都收敛.由定理2,可知 是收敛的.由定理6知,若级数绝对收敛,则它本身一定收敛,但反之不真.

例2 判别下列级数的收敛性,若级数收敛,指出是绝对收敛还是条件收敛.

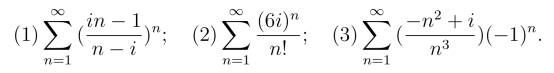
解 (1)因|αn|≥1不趋向于零,由定理5,该级数发散.

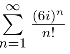(2)因由正项级数的比值审敛法知收敛,故原级数收敛,且为绝对收敛.

(3)其实部级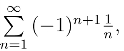数为 虚部级数为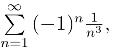由交错级数判别法可知它们都收敛,于是由定理3,得所给原级数收敛.

又由于由调和级数的发散性和正项级数比较判别法得,所给原级数非绝对收敛,因而条件收敛.