6.2.5 保侧性
对于扩充复平面上的任一个圆周(含直线),它的任意有序的不同三点都给出了该圆周的一个绕向.
设z1,z2,z3为普通圆周C上的任意三个不同点.动点z沿圆周C从点z1移动到点z2 有两个绕向,一个过点z3,另一个不过z3,这表明沿圆周C 从点z1到z2的方向不是惟一的,不能用它来表示C的方向.可是当动点z沿C移动时,依次通过点z1,z2,z3 的绕向是惟一的.于是可用C 上有序的三点z1z2z3 来表示这个绕向,即C的方向(如图6.9所示),同理C的这个方向也可用有序的三点z2z3z1或z3z1z2 来表示,逆序排列都表C的相反方向.
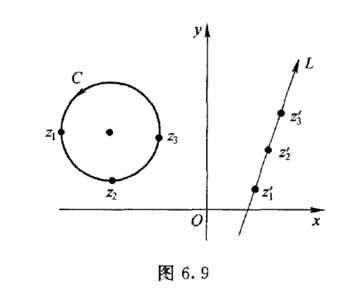
在扩充复平面上直线的两端都通向点∞,可将它看作在点∞闭合的圆周.这种圆周的绕向(即直线的方向)也可用在它上面的有次序的三个不同点来表示.如(图6.9)中,z′1z′2z′3给出了直线L的方向；把它看作圆周,其绕向是沿L依次通过点z′1,z′2,z′3和点∞,再从直线的另一端返回到点z′1 的方向.这个方向也可用z′2z′3z′1 或z′3z′1z′2来表示,逆序排列表示L的相反方向.
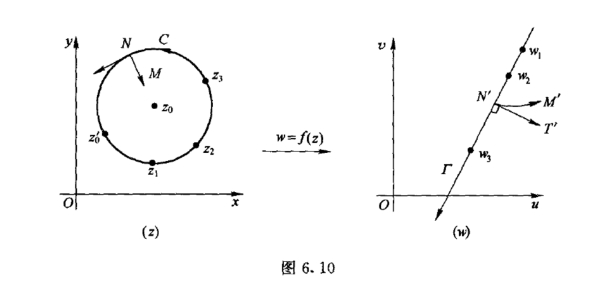
由分式线性映射的保圆性和边界对应原理知,当某分式线性映射w =f(z)将圆周C上的不同三点z1,z2,z3分别映射为w1,w2,w3时,C将映射为过点w1,w2,w3的圆周(包括直线)Γ.这时可设C为z = z(t)(α ≤t ≤β),C的方向由z1z2z3 给出,其中zk = z(tk).wk = f[z(tk)](k = 1,2,3;t1 ＜t2 ＜t3).当t增加时,动点z将沿C 依次通过点z1,z2,z3,对应点w = f[z(t)]将沿Γ 变动,且依次通过点w1,w2,w3给出了Γ的绕向(如图6.10 所示).
因此,对于扩充复平面上任一有向圆周,若给出它的一个方向,经分式线性映射后,仍为有向圆周.
扩充复平面上任一个有向圆周C把该平面分成以C为边界的两个区域,按照这两个区域的位置,分别称为C的左侧(内侧)和右侧(外侧).当C为直线时,点∞在C上,它既不属于C的左侧,也不属于C的右侧.下面证明,分式线性映射将扩充复平面上的有向圆周映射为有向圆周的同时,对有向圆周还具有保侧性.
定理5 若分式线性映射将扩充复平面上的有向圆周(含直线)C映射为有向圆周Γ,则它将C的左侧映射为Γ的左侧,将C的右侧映射为Γ的右侧.
证明 先证C为普通圆周,Γ为直线的情形(图6.10).这时,C 上有一点z′0映射为Γ上的点∞.于是在有向圆周C的左侧任取一点M,过点M的C的直径与C的两个交点中至少有一个映射为点∞,可设该点为N,有向线段
被映射为有向圆弧
或有向直线段N′T′.由于分式线性映射的保角性,有向圆周C在点N的切矢量到
的夹角将等于有向直线Γ 到
的夹角,使点M的对应点M′也在Γ 的左侧.由于所取点M为有向圆周C左侧的任意一点,因此C左侧的所有点都映射到有向直线Γ的左侧.
同理可证C的右侧一定被映射到Γ的右侧,以及C为直线,Γ为普通圆周的情形.
对于C和Γ都为直线的情形,可设该分式线性映射将C上有序的三个不同点z1,z2,z3依次映射为Γ上的点w1,w2,w3.于是该映射可表示为
(w1,w2,w,w3)=(z1,z2,z,z3),
可分解为分式线性映射
(1,i,η,-1)=(z1,z2,z,z3)
和
(w1,w2,w,w3)=(1,i,η,-1)
的复合映射,这两个映射分别将C映射为单位圆周,再将单位圆周映射为Γ.由于上面已经证明的结论对这两个分式线性映射都成立,因此对其复合映射也成立.
对于C和Γ都为普通圆周的情形,只须在实轴上取点η = 1,0,-1来构造所给分式线性映射的复合映射,可得同样的结果.
由于分式线性映射是一一对应的映射,其逆映射也是分式线性映射,将把Γ的左侧和右侧分别映射到C的左侧和右侧.这就保证了Γ左侧(右侧)的点与C左侧(右侧)的点是--对应的.
推论 设D为以任一个圆周(或直线)C为边界的区域,z0为D内任一定点.若某分式线性映射将C 映射为Γ,且将z0映射为w0,则该映射将D映射为w0所在的区域D′,D′的边界为Γ.
例2 试说明w =f(z)=
将区域D
映射为w平面上什么区域.
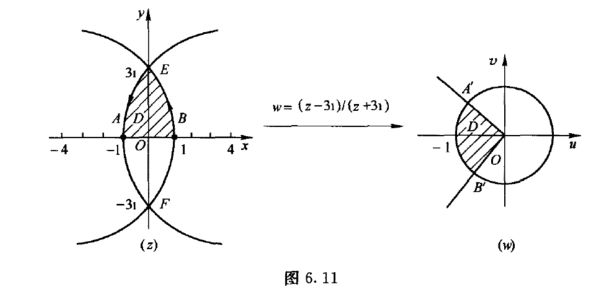
解 由于f(3i) = 0,f(-3i) = ∞,因此圆周|z+4| = 5,|z-4| = 5 都被映射为过原点的直线.
由f(-1)=
(记为A′),则圆弧
映射为线段
又由f(1)= 
(记为B′),则圆弧
映射为线段
在AB上取点z =0,由于f(0)=-1,得线段
映射为圆弧
由分式线性映射的保侧性,区域D′应当位于有向边界
的左侧,从而完全确定了区域D′(图6.11).