1.2.4　复数的运算性质

1.2.4　复数的运算性质

以上我们介绍了复数的共轭复数、复数的模以及四则运算,下面我们列出这些运算所具有的性质,这些性质很容易由定义、几何意义及运算法则得出.

(1) 设z =x+iy,由(图1-1),我们有不等式

|x|≤|z|,|y|≤|z|,|z|≤|x|+|y|,

-|z|≤Rez ≤|z|,-|z|≤Imz ≤|z|.

(2) 根据三角形两边之和大于第三边（图1-2）,我们可推出复数的三

角不等式：

|z1+z2|≤|z1|+|z2|.

我们知道,|z1-z2|表示点z1与z2之间的距离,又三角形两边之差小于第三边（图1-3）有

||z1|-|z2||≤|z1-z2|.

(3) |z1z2|=|z1||z2|,

(4) |z|=||.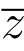

(5)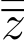 =z.

(6) z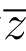 =|z|2 =|Rez|2+|Imz|2,|z|2 =|z2|.(https://www.daowen.com)

(7)

(8)

例4 求复数的模.

解 因为

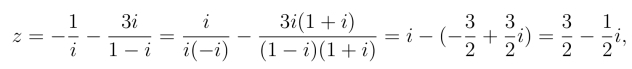
所以,

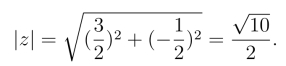
例5 若z为非零复数,证明：

证明 由于由和、差的模的不等式得到

例6 设z =x+iy,w = 求w的实部和虚部.

解