习题六
1.求下列映射在给定点z0处的伸缩率和转动角的主值.
(1)ω =z2,(z0 =i); (2)ω =sinz (z0 =π); (3)ω =ez (z0 =1+i).
2.在映射ω =z2下，求双曲线
C1 :x2-y2 =3; C2 :xy =2
的象曲线，并且利用该映射的保角性说明C1和C2在点z0 =2+i正交.
3.试求映射ω = f(z) = z2 +2z在z = -1+2i处的转动角，并说明它将z平面的哪一部分放大？哪一部分缩小？
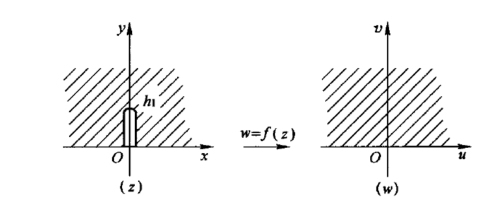
4.求下列区域在映射ω =i/z下的象.
(1)0 ＜Imz ＜1/2;(2)Rez ＞1 Imz ＞0.
5.求分式线性映射使点z = 1,i,-i分别映射为ω = i,1,-1,并求单位圆|z|＜1 在该映射下的象区域.
6.求把右半平面Rez ＞0映射为单位圆|ω|＜1的分式线性映射的一般形式.
7.求满足下列条件的分式线性映射ω =f(z).
(1)使|z|＜1映射为|ω|＜1,f(1/2)=0,f(-1)=i;
(2)使|z|＜1映射为|ω|＜1，且f(1/2)=0,arg f′(1/2)=-π/2;
(3)使Imz ＞0映射为|ω|＜1,f(i)=0,f(-1)=i;
(4)使Imz ＞0变为|ω|＜1,f(i)=0,arg f′(i)=π;
(5)f(-1)=0,f(0)=∞,f(1)=-1.
8.利用映射ω =(z+1)/(z-1)的特性,证明它使区域|z|＞1,Imz ＞0映射为-π/2 ＜arg ω ＜0;并作图.
9.试写出根式映射ω = 
的一个单值解析分支，使割去射线z =te2al(0 ≤t ≤∞) 的z平面映射为半平面a ＜Argω ＜π+a.
10.求一一对应的保角映射ω = f(z)使带有割痕l的上半z平面映射为上半ω 平面，如下图.
11.设有扇形区域D :|z|＜1,0 ＜arg z ＜π/4.求一个一一对应地保角映射使D映射为上半ω 平面D′ :Imω ＞0.
12.求一一对应的保角映射ω =f(z)，使带有割痕的单位圆映射为单位圆|ω|＜1,且使当θ →0+时,f(eiθ)→1,又当θ →2π-时,f(eiθ)→-1.
D :0 ＜Argz ＜2π,|z|＜1
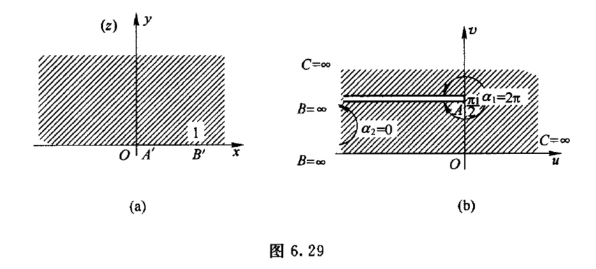
13.设L为半直线z = x(-∞≤x ≤a),D0为带形域-H ＜Imz ＜H(H ＞0)割去半直线L所构成的区域.试求一个一一对应的保角映射,使区域D0映射为上半ω 平面Imω ＞0.
14*.求下列区域在所给映射下的象
(1)D :0 ＜Imz ＜π;Rez ＞0(ω =cosh z);
(2)D :0 ＜Imz ＜π;Rez ＜0(ω =cosh z);
(3)D :0 ＜Rez ＜π;Imz ＞0(ω =cos z);
(4)D :-π ＜Rez ＜0;Imz ＞0(ω =cos z);
(5)D :-π/2 ＜Imz ＜π/2;Rez ＞0(ω =sinh z);
(6)D :-π/2 ＜Imz ＜π/2;Rez ＜0(ω =sinh z);
(7)D :-π/2 ＜Rez ＜π/2;Imz ＜0(ω =sin z);
(8)D :-π/2 ＜Rez ＜π/2;Imz ＞0(ω =sin z).
15.求将上半Z平面Imz ＞0一一对应地映射为角形域0 ＜arg ω ＜3π/2的保角映射ω =f(z),并使f(0)=0,f(1)=2,f(∞)=∞.
16.求将上半平面Imz ＞0一一对应地映射为图6.29(b)所给三角形区域的保角映射，并且使点z = -1,0,∞分别映射为该三角形的顶点A、B、C.其中A为ω =2πi.
17.求将上半z平面Imz ＞0一一对应地映射为半带形域D(D : Reω ＞0,0 ＜Imω ＜π)的保角映射ω = f(z)，且使z = -1,1,∞分别映射为三角形区域D的顶点ω1 =πi,ω2 =0,ω3 =∞.
18.试求在角形域0 ＜arg z ＜π/2内的调和函数φ(x,y),使它分别满足边界条件
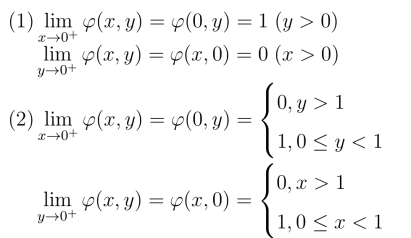
19.求ω = z2在z = i处的伸缩率和转动角.问：ω = z2将经过点z = i 且平行于实轴正向的曲线的切线方向映射成ω平面上哪一个方向？并作图.
20.一个解析函数所构成的映射在什么条件下具有伸缩率和转动角的不变性？映射ω =z2 在z平面上每一点都具有这个性质吗？
21.证明：映射
把圆周|z|=c 映射成椭圆：
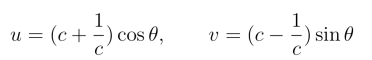
22.证明：在映射ω =elz下，互相正交的直线族Rez =c1 与Imz =c2依次映射成互相正交的直线族v =u tan c1 与圆族u2+v2 =e-2c2.
23.设ω =
,试证：φ=arg ω′(a).
24.求把上半平面Imz ＞0映射成单位圆|ω| ＜1的分式线性映射ω =f(z),并满足条件：
(1)f(i)=0,f(-1)=1;
(2)f(i)=0,arg f′(i)=0;
(3)f(1)=1,f(i)=
25.求把|z|＜1映射成|ω|＜1的分式线性映射，并满足条件：
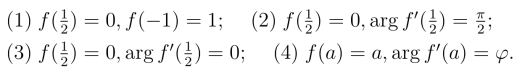
26.把点z = 1,i,-i分别映射成点ω = 1,0,-1的分式线性映射把单位圆|z|＜1映射成什么？并求出这个映射.
27.求出一个把右边平面Rez ＞0映射成单位圆|ω|＜1的映射.
28.证明儒可夫斯基映射
在圆外区域|z|＞a为保角映射，并且证明
(1) 对于任意r ＞a，它把圆周z = reiθ(0 ≤θ ≤2π)映射为ω 平面上椭圆
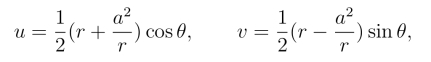
(2)*它把圆周|z| = a映射为线段v = 0,-a ≤u ≤a,并且把区域|z| ＞a映射为割去该线段的ω平面；又把区域|z|＞a,Imz ＞0 映射为Imω ＞0.
29*.求把上半z平面映射成ω平面中如下图所示的阴影部分的映射，并使x=0 对应于A 点，x=-1 对应于B 点.
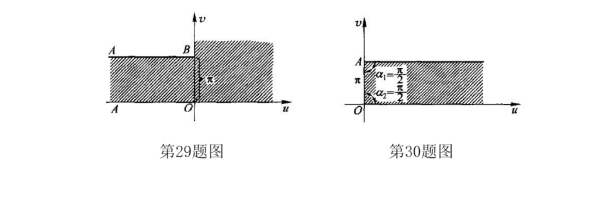
30*.求把下图中所示的阴影部分映射成上半平面的映射，并使A点对应于x=-1,O点对应于x=1.