8.5.1 解常系数线性常微分方程
1.用拉氏变换解初值问题的步骤如下：
1° 设方程的未知函数y =y(t)的拉氏变换为L[y(t)] = Y (p);
2° 对方程进行拉氏变换,利用拉氏变换的线性性质,微分性质（连带着初始条件）等,得到一个关于象函数Y (p) 的代数方程;
3° 解象函数的代数方程,解得Y (p);
4° 对Y (p),求其逆变换,得到Y (p) 的象原函数y(t) 就是该初值问题的解.
这一解法的示意图如下：
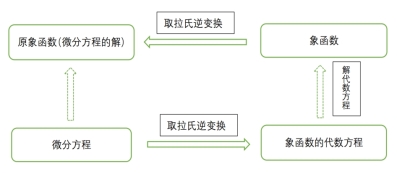
用拉氏变换解其它问题的步骤和上面的步骤大体相同.
例1 求方程y′′+4y =0满足初始条件y(0)=-2,y′(0)=4的特解.
解 设L[y(t)] = Y (p),方程两边取拉氏变换,得
由于
所以(8.5.1)式为
解得
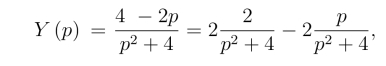
上式取拉氏逆变换,得到原方程的解
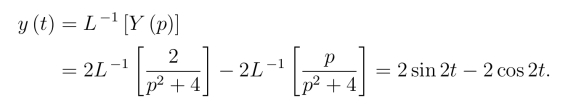
例2 求方程y′′-2y′-3y =4e2t 满足初始条件y(0)=2,y′(0)=8 的特解.
解 设L[y(t)] = Y (p).对方程两边取拉氏变换,得
由于
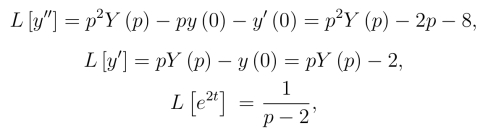
将它们代入(8.5.2)式,得
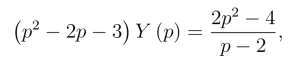
解得
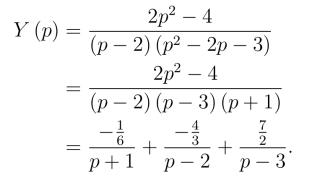
上式取拉氏逆变换,得到原方程的解
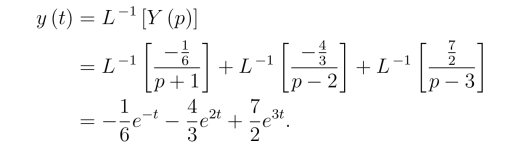
从上面的例题,我们已经看到了用拉氏变换求解常微分方程初值问题的方法.我们将在本章的评注中,对用高等数学中经典的方法解常微分方程初值问题和用拉氏变换方法解同样问题进行简单的比较.
2.用拉氏变换解常微分方程边值问题
例3 求方程y′′-2y′ + y =0满足边界条件y(0)=0 y(1)=2 的特解.
解 设L[y(t)] = Y (p).对方程两边取拉氏变换,得
由于
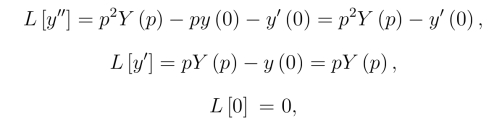
把它们代入(8.5.3)解得
由于y′(0) 为常数,(8.5.4)两端取拉氏逆变换,得
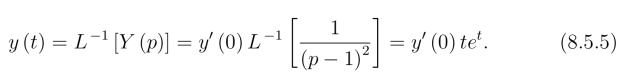
将y(1)=2 代入(8.5.5)式,可解得
这样我们就得到所求边值问题的解
从上面例题可以看出,要用拉氏变换解边值问题,可先把该问题看作初值问题求解.得到的解含有未知的初值,如(8.5.4)中的y′(0),该初值可由已给的边值(如本例中的y(1)=2)求得.