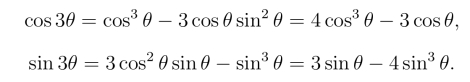1.2.3 复数的n次幂与n次方根
设z1 =r1eiθ1,z2 =r2eiθ2,··· ,zn =rneiθn是n个非零复数,用数学归纳法可以得到这n个复数的乘积为
特别地,当这n个复数相同时,我们把n个相同的复数z的乘积称为z的n次幂，
记作zn.设z =reiθ,则
zn =rneinθ =rn(cos nθ+i sin nθ).
当r =1时，即z =cos θ+i sin θ,有
(cos θ+i sin θ)n =cos nθ+i sin nθ.
这就是著名的棣莫弗(De Moivre)公式.
任意非零复数z,若有复数w,使得wn = z,则称w为z的n次方根,记作
下面我们来求根w的具体形式.设z =r(cos θ+i sin θ)
0,w =ρ(cos φ+i sin φ),根据棣莫弗公式,
ρn(cos nφ+i sin nφ)=r(cos θ+i sin θ),
又正弦函数、余弦函数的周期性,可得
ρn =r,cos nφ=cos θ =cos(θ+2kπ),sin nφ=sin θ =sin(θ+2kπ),
其中k为整数.于是
这样我们得到了z的取n个不同值的n次方根,
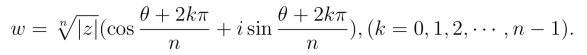(https://www.daowen.com)
不难验证,k取其它整数时,上述的n个值会重复出现,故z的n次方根只取上面n 个值.由于复数
的n个不同值的模都为
且对应相邻两个k的方根的辐角均相差
所以在几何上,复平面上
的n个不同值的n个点是以原点为中心,
为半径的圆的内接正n 边形的n个顶点.特别是z =1时,若令
则1 的n次方根为1,w,w2,··· ,wn-1.
例2 求
解 因为 1+i=
由n次方根公式得：
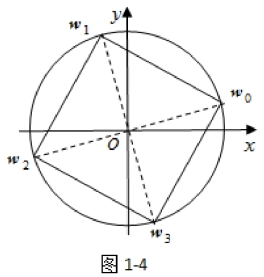
可得四个根分别为
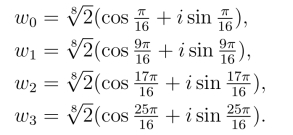
这四个根在复平面上内接于以原点为中心,
为半径的圆的正方形的四个顶点(图1-4).
例3 试用sin θ和cos θ表示cos 3θ和sin 3θ.
解 由棣莫弗公式,
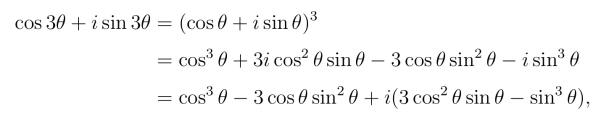
于是
