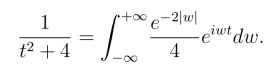7.1.2　傅里叶变换

7.1.2　傅里叶变换

本节主要研究将任意函数分解为正弦曲线的问题,我们知道如何将周期函数表示为一个傅里叶级数,因此,对于非周期函数,我们也希望找到类似的表达.

如果函数f(t)满足傅氏积分定理的条件,在f(t)的连续点处有

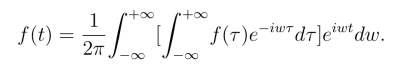
若令

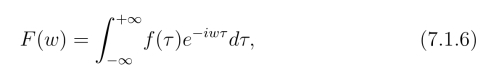
则

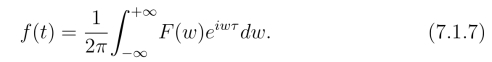
(7.1.6),(7.1.7)两式表明,f(t)和F(w)可以通过积分运算相互表示.

(7.1.6)称为f(t)的傅里叶变换式(简称傅氏变换),记为

F(w)称为f(t)的傅氏变换的象函数.

(7.1.7)称为F(w)的傅里叶逆变换式(简称傅氏逆变换),记为

f(t)=F-1[F(w)],

f(t)称为F(w)的傅氏变换的象原函数.通常称象函数F(w)和象原函数f(t)构成一个傅氏变换对,即

例2 求函数F(t)=的傅里叶变换,并验证F的傅里叶反演公式.

解 函数F(t) =在去除极点t = ±2i外解析,利用留数定理求傅里叶变换,并取积分的主值：

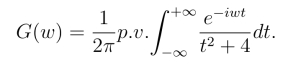
若w ≥0,在下半平面内用不断扩大的半圆周作闭合周线得到

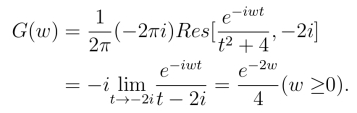
同理对于w＜0,在下半平面内作闭合周线,得

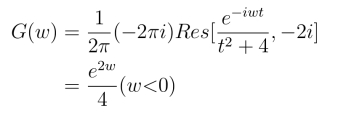
所以

为了验证傅里叶反演公式,我们计算

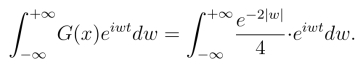
由对称性知,上式的虚部等于0,积分等于

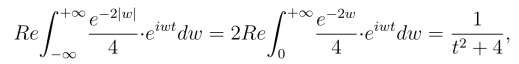
因此