5.1.2 孤立奇点的分类
下面,我们以洛朗级数为工具,对孤立奇点进行分类.如果z0是f(z)的孤立奇点,则在z0的某去心邻域0 ＜|z-z0|＜δ 内,函数f(z) 可展开成洛朗级数
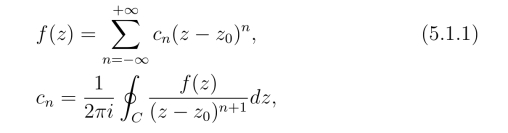
其中C为0 ＜|z-z0|＜δ内围绕z0的任一条正向简单闭曲线.
定义1 设函数f(z)在其孤立奇点z0(z0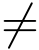 
∞)处的去心邻域的洛朗级数为式(5.1.1).
(1) 如果在洛朗级数中不含z-z0的负幂项,那么称z0为可去奇点.
(2) 如果在洛朗级数中只有有限多个z-z0的负幂项,且其中关于(zz0)-1 的最高幂为(z-z0)-m,即c-m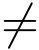 
0,那么称z0 为函数f(z) 的m 级极点.其中1级极点也称为简单极点.
(3) 如果在洛朗级数中含有无穷多个z -z0的负幂项,那么称z0为函数f(z) 的本性奇点.
由定义1可知,当z0为f(z)可去奇点时,f(z) 在z0的去心邻域0 ＜|z -z0|＜δ内的洛朗级数为
f(z)=c0+c1(z-z0)+c2(z-z0)2+··· ,
记右端级数的和函数为F(z),则F(z)在z0点是解析的,并且当z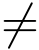 
z0 时,F(z)=f(z); 当z-z0时,F(z0)=c0,于是
若补充定义f(z0)=c0,则f(z)在z0点解析.
由以上分析可知,孤立奇点z0是f(z)的可去奇点的充分必要条件为
例如,z =0是函数
的可去起点,由于
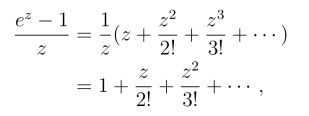
如果定义
在z =0的值为1,则
在z =0也解析.
今后,当z0为函数f(z)的可去奇点时,我们总把z0看作f(z)的的解析点,并且规定f(z0)=
如果z0为f(z)的m级极点,f(z)在z0 的去心邻域0 ＜|z-z0| ＜δ内的洛朗级数为
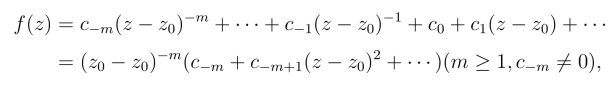
记φ(z)=c-m+c-m+1(z-z0)+c-m+2(z-z0)2+···,则φ(z)在圆域|z-z0|＜δ内解析,且
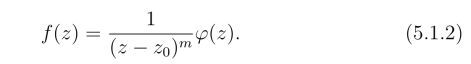
反之,若存在在点z0解析的函数φ(z)且φ(z0)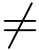
0,使式(5.1.2)成立,则z0是f(z)的m级极点.
当z0是f(z)的极点时,由式(5.1.2)可知
如果z0为f(z)的本性奇点,函数f(z)具有以下性质:
在z0的去心邻域内,对于任意给定的复数M,总可以找到一个趋于z0 的数列zn,使得
从而当z 趋于z0 时,f(z)的极限不存在,也不是∞（证略）.例如,函数f(z)在0 ＜|z|＜∞的洛朗级数
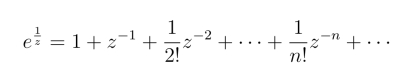
中含有无穷多个z的负幂项,从而z = 0为
的本性奇点.对给定的复数M = i,选取数列zn =
则当n →∞时,zn →0,而
若给定复数M = -i,可选取数列zn =
当n →∞时,zn →0,而
这样,当z 趋于z0 时,
的极限不存在,也不是∞.
由于上面我们已经讨论了函数f(z)在孤立奇点的极限的所有情况,因此我们可以通过函数在孤立奇点的极限情况来判断孤立奇点的类型.如果函数f(z)在其孤立奇点z0的极限
(1) 存在,则z0为f(z)的可去奇点;
(2) 为∞,则z0为f(z)的极点;
(3) 不存在也不为∞,则z0为f(z)的本性奇点.
对于极点,我们可以通过函数的零点来判别.