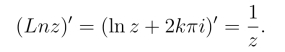2.4.2 对数函数
定义2 我们称复指数函数z =ew(z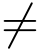 
0)的反函数为对数函数,记作
w =Lnz.
为导出其计算公式,设w =u+iv,θ =arg z,z =reiθ,则由z =ew得
比较等式两边得
u=ln r,v =θ+2kπ,k ∈Z
那么复数z的对数的所有值为
w =Lnz =ln r+i(θ+2kπ),
其中k为整数.
由于Argz = arg z +2kπ(k为整数)是无穷多值的,可见对数函数w =Lnz是一个多值函数,当k取不同值时,可得它的不同的单值分支,并且每两个单值分支都相差2πi 的整数倍.我们通常只讨论k = 0所对应的单值分支,即当k = 0时,我们称w = ln r+i arg z 为w = Lnz的主值.也就是说,对应于z的辐角主值的对数值,称为复数z 的对数的主值.记为ln z,它是单值函数,即
ln z =ln r+i arg z-π ＜arg z ≤π.
从而有
Lnz =ln z+2kπi(k为整数).
式中ln r是正实数的对数,当z = x ＞0时,ln r = ln x,arg z = 0.这说明主值对数是正实数对数在复数域内的推广.
对应于每一个固定的k,可以得到一个单值函数,称为w =Lnz的一个分支.例如固定整数为k0时,对应的单值分支可表示为
w =ln z+2k0πi.
另外,实变数对数函数的运算性质对于复变数对数函数仍然成立：
设z2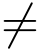 
0,则
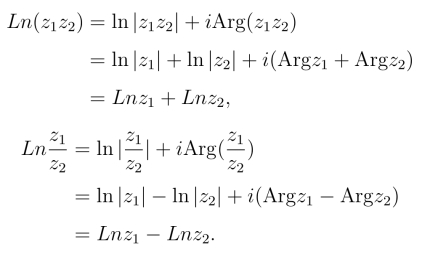
注意: 以上两等式的理解为,当每一式右端的对数取其一个分支所确定的值后,左端也一定有一个分支的值与之相等.
例2 求Ln(-2),Lni,Ln(1+i)及其主值.
解因为Ln(-2)=ln|-2|+i arg(-2)+2kπi=ln 2+2(k+1)πi,(k为整数),所以Ln(-2)的主值为
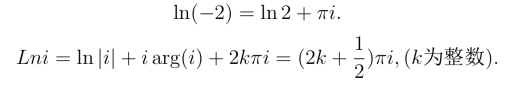
所以它的主值为
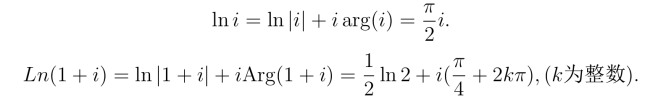
它的主值为
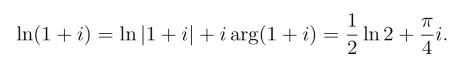
例3 设z1 =-2,z2 =2i,试计算下列复数z2,-z2,z1z2,
的对数主值.
解
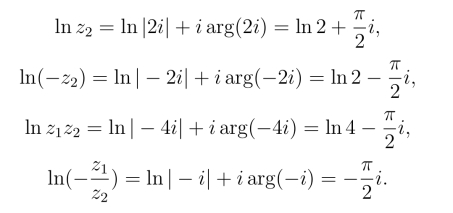
注1 由上述例3可以看出,对任意的z1和z2,ln z1z2 =ln z1+ln z2,
ln z1-ln(-z2) 不一定成立.因此,多值函数的运算性质对主值函数不一定成立.
注2 实变数的对数函数与复变数的对数函数有两点差别:
(1) 实变数的对数函数的定义域是全体正实数的集合,而复变数的对数函数的定义域是全体非零复数的集合;
(2) 实变数的对数函数是单值函数,而复变数的对数函数是无穷多值的函数.
我们再来讨论对数函数的解析性.对于主值ln z =ln|z|+i arg z,ln|z|除原点外处处连续,arg z 在原点及负实轴上都不连续.因为设z = x+iy,则当x ＜0 时,有
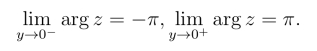
于是可知ln z在除去原点和负实轴的复平面内连续且单值.因为z = ew在区域-π ＜arg z ≤π 内的反函数w =ln z 是单值的,由反函数的求导法则可知
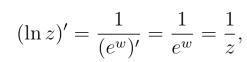
所以ln z在除去原点和负实轴的复平面内解析.
对于其他分支,由于它们之间仅差2πi的整数倍,因此在除去原点与负实轴的复平面内解析,且有相同的导数,即
