9.2　希尔伯特变换的性质

9.2　希尔伯特变换的性质

1.线性性质

若a,b为任意常数,且 则有:

2.位移性质

3.希尔伯特变换的希尔伯特变换

此性质表明此两重希尔伯特变换仅是使原函数添加上了一个负号,由此可得：

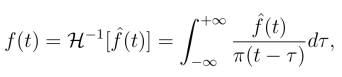
4.逆希尔伯特变换f(t)为的卷积,可表示为：

其中

5.奇偶特性

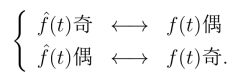
即若原函数f(t)为奇(偶)函数,则其希尔伯特变换为偶(奇)函数,即

6.能量守恒(https://www.daowen.com)

根据帕塞瓦尔定律,我们可以得到：

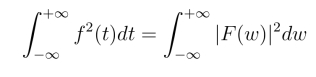
和

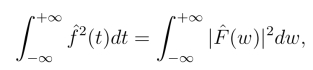
因而,我们可以得到：

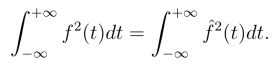
7.正交性质

由于f(t)和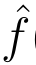(t)分别为解析函数Z(t)的实部和虚部,我们可以得到：

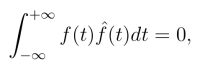
即正交性.

8.调制性质

对于任意函数f(t),若其傅里叶变换有以下形式：

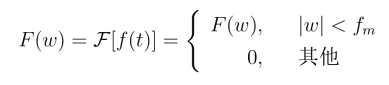
则有

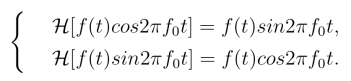
9.卷积性质

另外,希尔伯特变换具有周期性和同域性,即希尔伯特变换不改变原函数的周期性,也不改变域表示,而不像傅里叶变换那样,把信号从时域改变为频域表示.