2.4.5　反三角函数和反双曲函数

2.4.5　反三角函数和反双曲函数

三角函数的反函数称为反三角函数.

定义7 设

z =sin w,

我们称w为z的反正弦函数,记作

w =Arcsinz.

由于

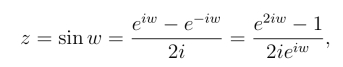
可得

(eiw)2-2izeiw-1=0,

解之得

于是有

类似地可定义反余弦函数、反正切函数和反余切函数：

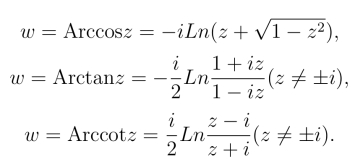
由于根式函数、对数函数都是多值函数,所以它们都是多值函数.在相应地取了单值连续分支以后,由反函数的求导法则,可以得到:(https://www.daowen.com)

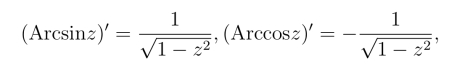
由对数函数的求导法则,可得

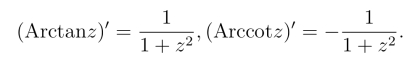
双曲函数的反函数称为反双曲函数,与反三角函数的推导过程类似,可

推出各反三角函数的表达式.

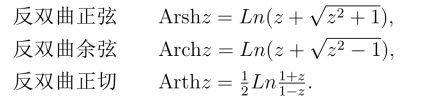
例6 解方程|tanh z|=1.

解 tanh z =

两边平方,并令e2z =u+iv,

(u-1)2+v2 =(u+1)2+v2 或u=0,

因为u=Re(e2z)=e2Re(z)cos[2Im(z)]=0,

cos[2Im(z)]=0,

计算得

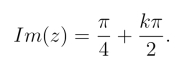
故|tanh z|=1的解是满足Im(z)= 的所有复数z.