5.2.4 函数在无穷远点的留数
2026年01月14日
5.2.4 函数在无穷远点的留数
设函数f(z)在z = ∞的去心邻域R <|z| <+∞内解析,C 为该邻域内包含圆周|z| = R 的任一条简单闭曲线,则闭曲线C环绕z = ∞的正向,就是C环绕z =0的负向,因此我们可定义函数f(z) 在z =∞的留数为
定义2 设z =∞是函数f(z)的孤立奇点,f(z)在z =∞心邻域R <|z|<+∞内解析,f(z)在z =∞的留数
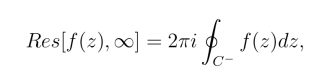
其中C为包含圆周|z|=R只的任一条正向简单闭曲线.
设函数f(z)在z = ∞的去心邻域R <|z| <+∞内的洛朗级数为式(5.1.5),由洛朗级数的系数公式有
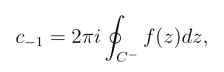
从而有
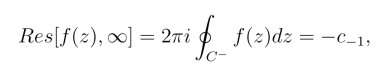
即f(z)在∞点的留数等于它在∞点的去心邻域R <|z| <+∞内洛朗级数中z-1 的系数的相反数.
定理3 若函数f(z)在有限复平面内只有有限个孤立奇点z1,z2,··· ,zn,则z =∞也是f(z)的孤立奇点,且
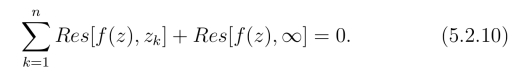
证明令R = max{|z1|,|z2|,··· ,|zn|},则f(z)在点z = ∞的邻域R <|z| <+∞内解析,z = ∞是f(z)的孤立奇点.设C 为包含圆周|z| = R的任意正向简单闭曲线,由留数定理及在无穷远点的留数定义有
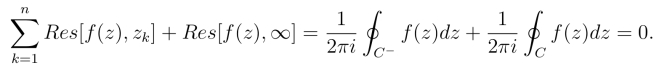 (https://www.daowen.com)
(https://www.daowen.com)
由函数在无穷远点的留数定义及定理2可得
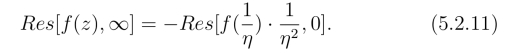
上式可用来计算函数f(z)在无穷远点的留数.
例8 计算积分![]() C为正向圆周: |z|=3,
C为正向圆周: |z|=3,
解 被积函数f(z)=![]() 在|z|=3的内部有6个1级极点
在|z|=3的内部有6个1级极点
![]()
在|z| = 3的内部.直接使用式(5.2.6),要计算6个1级极点的留数,比较麻烦.
在|z|=3的外部的奇点为1级极点z =4及z =∞,且
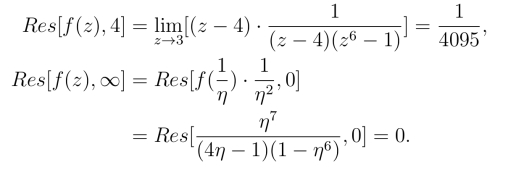
由定理3,得
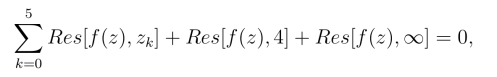
从而有