习题四
1.复数列αn =an+ibn →0 ⇔|an|→0,为什么？
2.试举例当通项αn →0(n →∞)时，复数项级数α1+α2+···+αn+···可能发散.
3.判别下列复数列的收敛性，且当收敛时求出其极限，其中n →∞
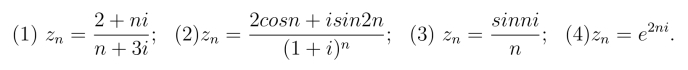
4.判断下列级数的绝对收敛和收敛性.
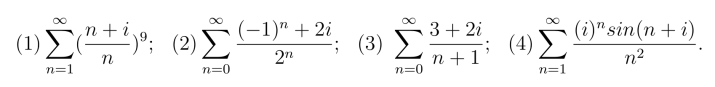
5.幂级数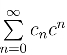
能否在z =2i 收敛而在z =1发散？为什么？
6.在逐项积分公式(4.2.6)中，为什么其积分下限必须是其收敛圆的中心z0且不必写出其积分路径？
7.求下列幂级数的收敛圆的中心和收敛半径.
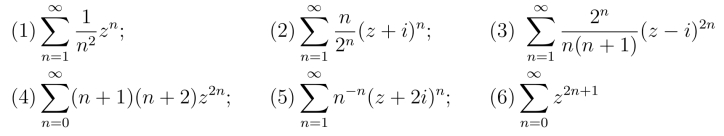
8.设当n →∞时，数列λn = |an+1/an| 收敛于λ.试证下列三个幂级数的收敛半径都为R=1/λ.
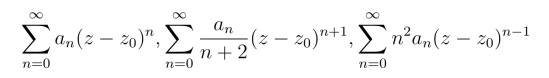
9.求函数f(z) = 1/[(z-1)(z-2)]在点z0 = i的泰勒级数展开式的收敛半径.
10.一元实函数f(x) = (1 + x2)-1在实轴上处处有任意阶导数,他在点x0 = 0可以展开成实数向的泰勒级数，使用本节定理说明其收敛半径为什么是R=1而R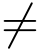
∞?
11.设当z = 0时f(z) = 1;当z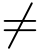 
0时f(z) = sin(z)/z.试说明f(z) 在整个复平面解析.
12.求下列函数在点z0 =0处的泰勒级数展开式及其收敛半径.
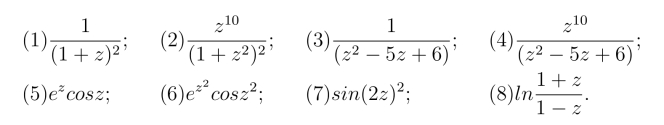
13.将下列函数在指定点出展开成泰勒级数，且指出其收敛半径.
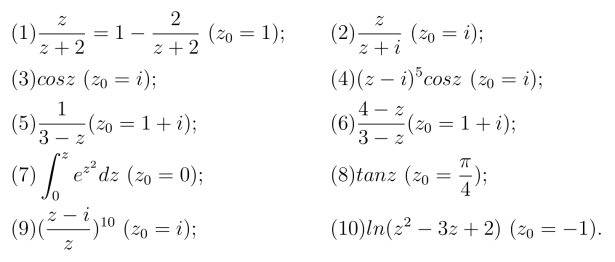
14.函数f(z)在上述各个环域内有不同的洛朗级数展开式，这与它的洛朗级数展开式的惟一性矛盾吗?为什么?
15.以点z0 =i为中心过函数f(z)=1/[z(z+1)(z+2i)]的奇点作圆周,试说明f(z)在以点z0为中心的哪些环域内可以展开成洛朗级数?
16.求函数f(z)=i/[(z-i)(z-2i)]在下列环域内的洛朗级数展开式.
(1)1 ＜|z|＜2;(2)2 ＜|z|＜∞;(3)0 ＜|z-i|＜1.
17.求函数f(z)=1/[z(z+2)2]在下列环域内的洛朗级数展开式.
(1)0 ＜|z+2|＜2;(2)2 ＜|z+2|＜∞.
18.试说明下列每一个函数在点z =0和z =∞的去心邻域的洛朗级数展开式是一样的,并且求出其展开式.
(1)z3e1/z;(2)z4sin(1/z);(3)z-10cosz.
19.将下列函数在指定环域内展开成洛朗级数,且计算其沿正向圆周|z|=6 的积分值I.
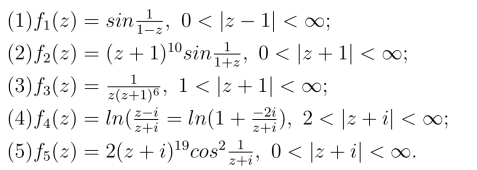
20.下列数列是否收敛?若收敛，求出极限.
21.判别下列级数的绝对收敛性与收敛性
22.下列说法是否正确?为什么?
(1)每一个幂级数在它的收敛圆周上处处收敛;
(2)每一个幂级数的和函数在收敛圆内可能有奇点;
(3)每一个在:。连续的函数一定可以在z0的邻域内展开成泰勒级数.
23.求下列幂级数的收敛半径R.
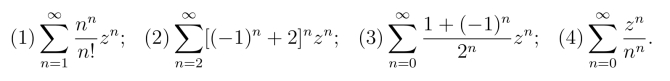
24.求幂级数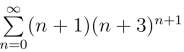
的收敛半径、收敛圆及和函数.
25.如果
的收敛半径为R,证明
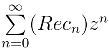的收敛半径≥R.
26.设级数
收敛，而
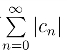发散,证明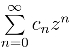
的收敛半径为1.
27.如果级数
在它的收敛圆的圆周上一点z0 处绝对收敛，证明它在收敛圆所围的闭区域上绝对收敛.
28.试求满足微分方程f′(z) = zf(z)的中心为0的幂级数,并求其收敛半径.
29.将f(z) =
运用(1+z)2f(z) = 1的关系,展开为以0为中心的幂级数,再求其收敛半径.
30.函数
能否在圆环域0 ＜|z| ＜R(0 ＜R ＜+∞) 内展成洛朗级数？为什么？
31.计算积分