6.5 小结
本章中首先介绍了解析函数导数的几何意义.设w = f(z)是区域D内的解析函数,z0 为D内一点.导数f′(z)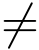 
0的辐角arg f′(z0)是曲线C经过w =f(z)映射后在z0处的转动角.它的大小与方向跟曲线C的形状与方向无关.|f′(z0)| 是经过映射w = f(z)后通过z0的任何曲线C在z0的伸缩率,它与曲线C的形状与方向无关.然后给出了曲线的切线方向和两条曲线的夹角的定义.
设w = f(z)为区域D内的解析函数,z0为D内一点,如果f′(z0)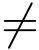 
0,那么通过z0的任何两条曲线C1与C2 之间的夹角,在其大小和方向上都等同于经过w = f(z) 映射后跟C1与C2对应的曲线Γ1与Γ1之间的夹角,即映射w = f(z)具有保持两曲线间夹角的大小和方向不变的性质,称为保角性.凡具有保角性和伸缩率不变性的映射称为保角映射.
本章重点讨论了分式线性映射.分式线性映射w = 
可以看成是由下列各映射复合而成：
1°ξ =z+b,平移变换；
2°η =aξ,旋转与伸缩变换；
3°w =
反演变换.
由于它们在扩充平面上都是一一对应,且具有保角性,保圆性,保对称性,保交比性和保侧性,因此,分式线性映射也具有这些性质.
利用保交比性,可以用三对相异的对应点写出所求的分式线性映射.设三个相异点z1,z2,z3对应于三个相异点w1,w2,w3,则分式线性映射为
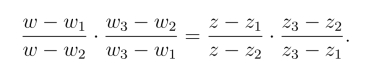
本章中介绍了三种典型的分式线性映射.
(1) 上半平面映射成单位圆内部的映射,它的形式是
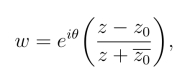
其中θ为实数,z0为上半平面内映射成圆心w =0的点.
(2) 单位圆映射成单位圆的映射,它的形式是
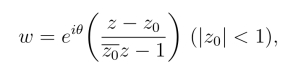
其中φ为实数,z0为单位圆|z|＜1内的任意一点.
(3) 上半平面映射成上半平面的映射,它的形式是
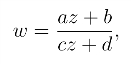
其中a,b,c,d都为实常数,且ad-bc ＞0.
本章还介绍了几个初等函数所构成的映射.由幂函数w = zn所构成的映射的特点是：把以原点为顶点的角形域映射成以原点为顶点的角形域,但张角变成了原来的n 倍.因此,如果要把角形域映射成角形域,常利用幂函数,根式函数w =
是幂函数z = wn的反函数,它所构成的映射把角形域映射成角形域,但张角缩小到
由指数函数所构成的映射的特点是：把水平的带形域0 ＜Imz ＜a(a ≤2π)映射成角形域0 ＜argw ＜a.因此,如果要把带形域映射成角形域,常利用指数函数.对数函数w = ln z 是指数函数z = ew的反函数,它所构成的映射把角形区域α ＜argz ＜β(-π ≤α ＜β ≤π) 映射为带形区域α ＜Imw ＜β.
应根据区域的形状选取适当的映射,有些问题还需要用到上面的多个映射进行复合.