4.2.3 收敛半径的求法
由阿贝尔定理可知,收敛半径一定存在,当R=∞时,级数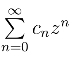
在整个复平面收敛,当R=0 时,级数只在z =0收敛.
关于收敛半径的求法,我们有下面的结论:
定理2(比值法) 设幂级数为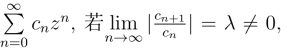
则收敛半径
证明 由于
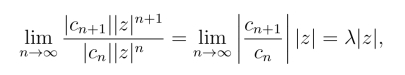
故知当|z|＜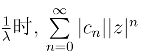 
收敛.从而级数
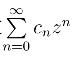在圆|z|=
内收敛且绝对收敛.
再证当|z| ＞
时,级数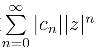
发散.假设在圆|z| =
外有一点z0,使级数
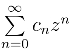收敛.在圆外再取一点z1,使|z1|＜|z0|,那么根据阿贝尔定理,级数
必收敛.然而
所以
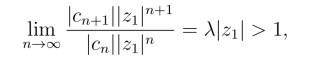
这跟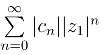
收敛相矛盾,即在圆周
外有一点z0 使级数
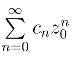收敛的假定不能成立.因而
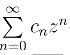在圆
发散.因此收敛半径
定理3(根值法) 若
则收敛半径
证明从略.
注意,定理中的极限是假定存在的而且不为零.若λ = 0,则对任何z,级数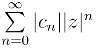
收敛,从而级数
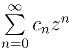在复平面内处处收敛,即R = ∞.若λ = +∞,则对于复平面内除z = 0以外的一切z,级数
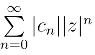都不收敛,因此
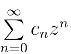也不能收敛,即R = 0.否则,根据阿贝尔定理将有z 
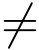0 使得级数
收敛.
例2 求下列幂级数的收敛半径：
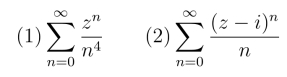
解 (1)因为
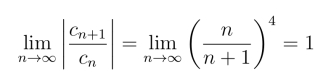
或
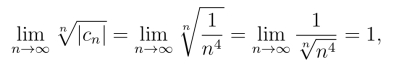(https://www.daowen.com)
所以收敛半径R=1.也就是原级数在圆|z|=1内收敛,在圆外发散.
(2)由于
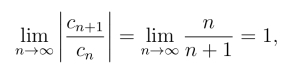
得R = 1.在上例(2)中,由于在收敛圆|z-i| = 1上,当z = i-1 时,原级数成为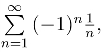
它是交错级数,根据莱布尼茨准则,级数收敛; 当z = i+1时,原级数成为
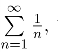它是调和级数,所以发散.这说明,在收敛圆周上可能既有级数的收敛点,也有级数的发散点.
例3 求下列幂级数的收敛圆及其收敛半径.
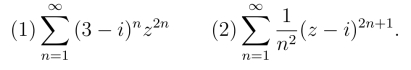
解 (1)该幂级数的奇次幂系数为零,不能直接使用定理2 或3.
令ζ =(3-i)z2得
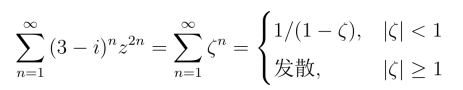
由例1可看出,其收敛域为|ζ| = |(3-i)z2| ＜1,即圆域
其收敛圆
收敛半径
它在其收敛圆周上处处发散.
(2)令(z-i)2 =ζ,则得
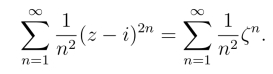
由定理2可求出上式右端的幂级数收敛半径R = 1,且在圆|ζ| = 1 的内部处处绝对收敛,在圆的外部发散.于是可设
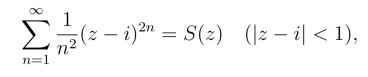
上式两端乘以(z-i),则有
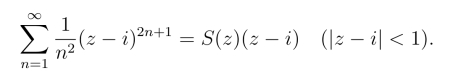
由|ζ| = |(z -i)2| = 1,得|z -i| = 1,因此级数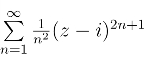
的收敛半径R=1,收敛圆为|z-1|=1.由于在收敛圆上,其绝对值级数
为收敛级数,所以该幂级数在圆周|z-i|=1 处处绝对收敛.