习题九

1.证明上述性质中每个希尔伯特变换性质.

2.利用欧拉公式和希尔伯特变换直接证明：如果|w|＜W1,则coswxcosW1x的希尔伯特变换是coswxsinW1x.

3.设f(z)在包含单位圆盘|z| ≤1的区域内解析,证明：对于任意常数w,g(x)=f(eiwx)+f(e-iwx)的希尔伯特变换是-i[f(eiwx)-f(e-iwx)].[提示：利用麦克劳林级数]

4.理论物理学家经常用到以下等式：

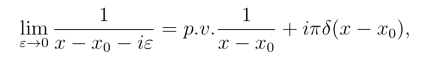
其中p.v.是函数的柯西主值,δ(x-x0)是狄拉克δ函数,它是一个理想化的函数,对任意的连续函数f(x),具有如下性质：

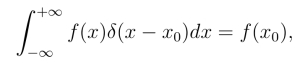
将原式两边同时乘以f(x),并在(-∞,+∞)上进行积分,交换极限与积分顺序,可以得到：

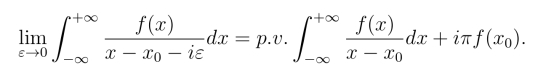
严格的说,后式是对前式的一种细化.

(a)假设f(x)在Imz ≥0时解析,在无穷远处趋于0 的速度充分快,使得它沿上半平面上的半圆周C+p 上的积分趋于0,试推导细化之后的等式.

(b)求极限