1.2.2 复数的乘法和除法
两个复数z1 =x1+iy1和z2 =x2+iy2的乘法定义如下:
z1z2 =(x1+iy1)(x2+iy2)=(x1x2-y1y2)+i(x2y1+x1y2).
我们称z1z2为z1与z2的积.两个复数作乘积时,可按多项式的乘法法则进行,注意结果中的i2 =-1.特别地,
zz=(x+iy)(x-iy)=x2+y2 =|z|2.
定义复数的除法时,即是要找到一个复数z = x+iy使得zz2 = z1,其中z2 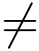 0,我们称复数z =x+iy为z1除以z2的商,记作
0,我们称复数z =x+iy为z1除以z2的商,记作![]() 从定义可推出
从定义可推出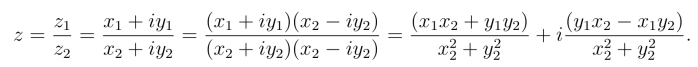
利用复数的三角形式或指数形式讨论复数的乘除法,可以进一步了解乘法、除法的几何意义,而且在进行复数乘除运算时,常常要比用代数形式方便.
设z1 = r1(cos θ1+i sin θ1),z2 = r2(cos θ2+i sin θ2)是两个非零复数,由复数乘法定义
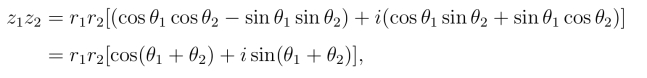
这是复数乘积的三角形式,最后一步用到了三角函数的和角公式.相应的指数形式为
![]()
上式说明,z1z2所对应的向量是把z1所对应的向量伸缩|z2|=r2倍,然后再旋转一个角度θ2 =arg z2 得到的.这样我们就有
|z1z2|=r1r2,
Arg(z1z2)=Argz1+Argz2.
第二个等式应该理解为两个集合的相等.于是我们得到复数的乘法法则:两个复数相乘,乘积的模等于它们的模的乘积,乘积的辐角等于它们的辐角的和.当|z2| = 1 时,只需要旋转一个角度arg z2.特别地,iz相当于将z所对应的向量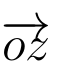 沿逆时针方向[1]旋转
沿逆时针方向[1]旋转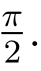
用三角形式和指数形式表示除法时,先假设z2 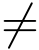 0,而
0,而
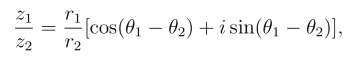
这是复数商的三角形式.相应的指数形式为
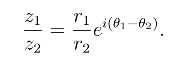 (https://www.daowen.com)
(https://www.daowen.com)
同样地,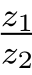 所对应的向量是把z1所对应的向量伸缩
所对应的向量是把z1所对应的向量伸缩![]() 倍,然后再顺时针旋转一个角度θ2 =arg z2得到的.这样我们就有
倍,然后再顺时针旋转一个角度θ2 =arg z2得到的.这样我们就有
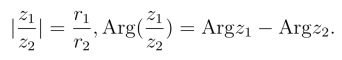
于是得复数的除法法则: 两个复数相除,商的模等于分子的模与分母模的商,商的辐角等于分子的辐角与分母的辐角的差.
例1 设![]()
解 z1,z2的三种表达形式为
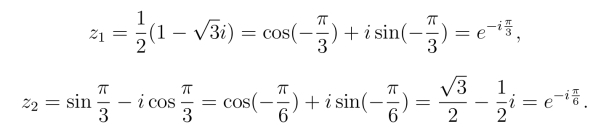
由复数代数形式的乘法和除法公式得:
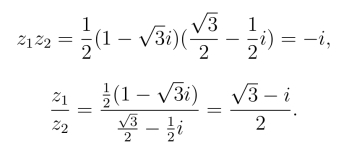
用三角形式、指数形式的运算得:
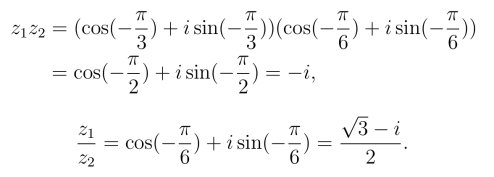
或
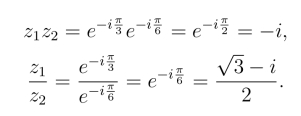
不难证明,复数的加法和乘法同样遵循下列运算规律:
(1) 加法交换律:z1+z2 =z2+z1;
(2) 加法结合律:(z1+z2)+z3 =z1+(z2+z3);
(3) 乘法交换律:z1z2 =z2z1;
(4) 乘法结合律:(z1z2)z3 =z1(z2z3);
(5) 乘法对于加法的分配率:(z1+z2)z3 =z1z3+z2z3.
