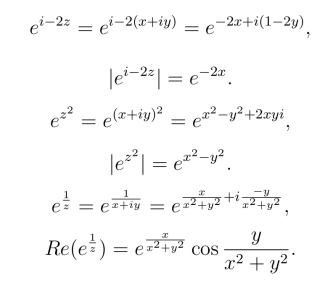2.4.1　指数函数

2.4.1　指数函数

从上节例2可知,f(z)=ex(cos y+i sin y)在整个复平面上解析,且f′(z)=f(z).容易验证f(z1+z2) =f(z1)+f(z2),据此我们给出复变指数函数的定义.

定义1 对任意的复数z =x+iy,定义指数函数为

w =ex(cos y+i sin y),

记作ez.

显然,|ez|=ex ＞0,而Arg(ez)=y+2kπ(k为整数),从而ez 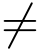0.当z 取实数,即y = 0,z = x时,ez = ex,此时它与实变量指数函数ex 一致,可见复指数函数是实指数函数的推广.当z取纯虚数,即x = 0,z = iy 时,得到欧拉(Euler)公式

ez =eiy =cos y+i sin y.

由定义,容易验证指数函数ez具有下列性质：

(1) 复变量指数函数ez在整个复平面内都有定义,且在整个复平面内解析,有

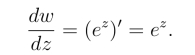
(2) ez满足加法、减法定理,对于任意的z1,z2,有

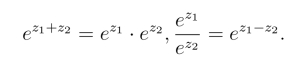
事实上,设z1 =x1+iy1,z2 =x2+iy2,则

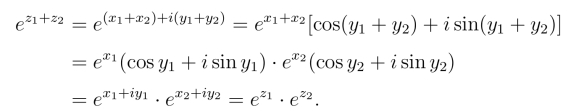
同理可证.但(ez1)z2 =ez1z2一般不成立.

(3) 由加法定理,可推出ez的周期性.对任意整数k,都有

因为

一般地,对任意整数k,都有

2πi是ez的周期且模最小,我们称2πi是ez的基本周期.因此,我们常说ez是以2πi为周期的周期函数.

(4)不存在.

例1 设z =x+iy,求

解 因为

所以其模|ez|=ex,实部Re(ez)=ex cos y.