6.1.1 曲线的切线方向和两条曲线的夹角
设C是z平面内的一条有向连续曲线,其参数方程为
z =z(t),α ≤t ≤β
C的正向取为t增大时,点z移动的方向.z(t) 是一个连续函数,若z′(t0) 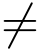 0,α <t0 <β,则z′(t0)就是曲线C在点z0 =z(t0)的切线方向(图6.1).
0,α <t0 <β,则z′(t0)就是曲线C在点z0 =z(t0)的切线方向(图6.1).
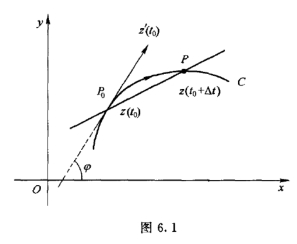
事实上,曲线C上P0点的切线就是割线P0P 当P沿曲线C趋于P0时的极限位置.
由于割线P0P的方向与表示
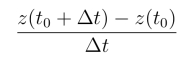
的向量的方向一致,其中z(t0+Δt) 与z(t0)分别为点P与P0 所对应的复数,当Δt →0时,点P沿C 无限趋向于点P0,因此
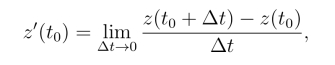 (https://www.daowen.com)
(https://www.daowen.com)
其方向与C的正向一致,如果我们规定这个向量的方向作为C上点z0处的切线的正向,则有
定义1 对于给定的有向光滑曲线C:z = z(t)(α ≤t ≤β),称复向量z′(t0)为曲线C在点z0 =z(t0)的切矢量,称Argz′(t0)为正实轴到矢量z′(t0)的夹角.
在定义1中,由于C是光滑曲线,因此z′(t0) 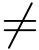 0,即切矢量总是存在的,Argz′(t0)实际上是正实轴方向绕原点旋转到切矢量z′(t0)的转动角.
0,即切矢量总是存在的,Argz′(t0)实际上是正实轴方向绕原点旋转到切矢量z′(t0)的转动角.
对于相交于一点的两条曲线的夹角,定义为这两条曲线在该点处切线的夹角(图6.2).
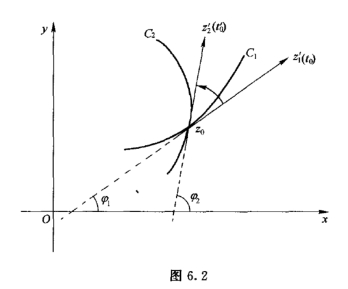
定义2 设有两条相交的有向曲线C1 和C2,它们的参数方程分别为z =zk(t)(αk ≤t ≤βk;k = 1,2),其交点为z0 = z1(t0) = z2(t′0),在z0处切矢量分别为z′1(t0)和z′2(t′0).我们称C1的切矢量z′1(t0)绕z0 旋转到C2的切矢量z′2(t′0)的转动角为C1到C2在点z0的夹角,记为∠C1z0C2.由于这个转动角可看作矢量z′1(t0)绕点z0 旋转到实轴正向再旋转到矢量z′2(t0) 的复合,因此可表示为
![]()
显然∠C1z0C2是多值的,且有∠C2z0C1 =-∠C1z0C2.
