5.4.2　辐角原理

5.4.2　辐角原理

下面讨论定理1中对数留数的几何意义.

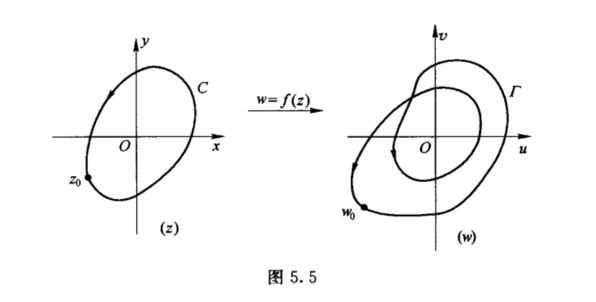
考虑变换w = f(z),当z沿简单闭曲线C的正向绕行一周时,对应点w在w平面内就画出一条连续的封闭曲线Γ; 它不一定是简单的闭曲线,它可以按正向绕原点若干圈,也可以按负向绕原点若干圈.由于f(z)在C上不为零,因此在w平面内Γ也不经过原点(图5.5).

设简单闭曲线C为z = z(t)(α ≤t ≤β),z0为C上一点(z0 = z(α) =z(β)),则函数f(z)关于闭曲线C的对数留数

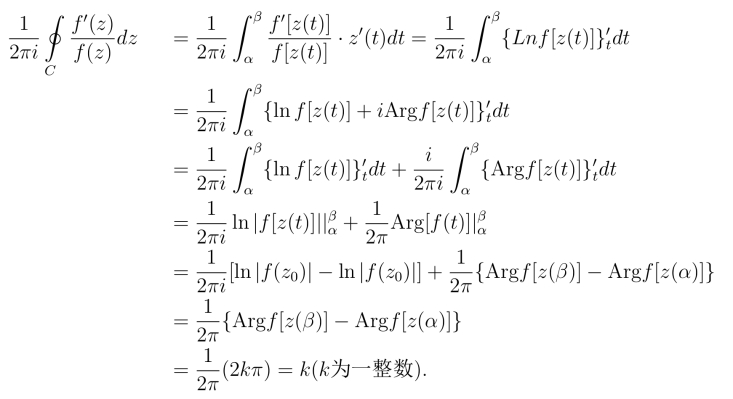
由此可见,函数f(z)关于C的对数留数的几何意义就是曲线Γ绕原点w =0回转次数的代数和(Γ绕w = 0逆时针转一周次数为1,顺时针转一周次数为-1).

称Argf[z(β)]-Argf[z(α)]为动点z沿闭曲线C一周函数F(z)的辐角的改变量,记作

于是定理1可叙述为

定理2(辐角原理) 若f(z)在正向简单曲线C上解析且不为零; 在C 的内部除去有限个极点外处处解析,则有

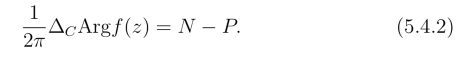
在定理2中,若P =0,则有

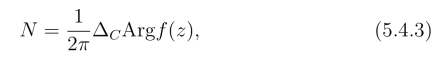
即当f(z)在简单闭曲线C上及C内解析且在C上不等于零时,f(z)在C内零点的个数等于乘以当z沿C的正向绕行一周f(z)的辐角的改变量.