7.4.1　卷积的定义

7.4.1　卷积的定义

卷积又叫褶积或旋积,是一种积分变换的数学方法,在许多方面得到了广泛的应用.

定义 若函数f1(t)与f2(t)在(-∞,+∞)上可积,则称积分

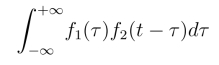
为函数f1(t)与f2(t)的卷积,记为f1(t)*f2(t),即

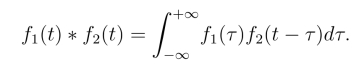
卷积的计算较为复杂,下面我们来解释计算过程.

(1)首先将两个函数都用τ来表示：f1(t)→f1(τ),f2(t)→f2(τ);

(2)对其中一个函数做水平翻转：f2(t)→f2(-τ);

(3)加上一个时间偏移量t,让f2(t-τ)沿着τ轴滑动;

(4)f1(t)*f2(t)是t的函数,如果对某些t,f1(τ)f2(t-τ)=0,则它们的积分值即卷积为0; 要求非0的卷积值,就要解出使得两函数f1(τ),f2(t-τ)同时不为0 的区间,我们再算出这个区间上两函数卷积值(通常与t 相关).

例1 设f1(t)=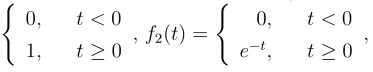求f1(t)*f2(t).

解 由于

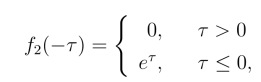
所以

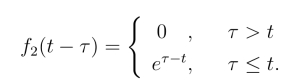
结合

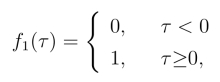
得到仅当t ≥0,0 ≤τ ≤t时,f1(τ)f2(t-τ)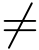0,所以