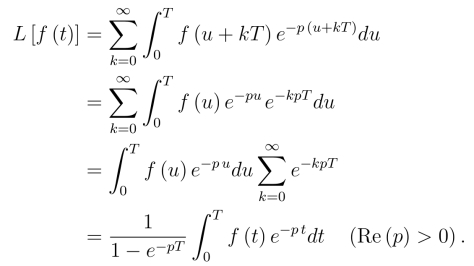8.1.3　一些常用函数的拉氏变换

8.1.3　一些常用函数的拉氏变换

例1 求函数f(t)=1的拉氏变换.

解

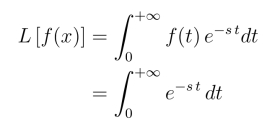
当Re(s)＞0时,显然

所以当Re(s)＞0时,

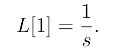
例2 求指数函数f(t)=e(kt)的拉氏变换(k为实常数).

解

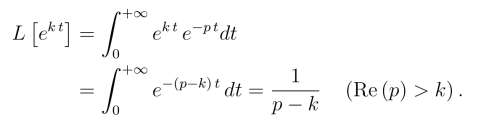
例3 求余弦函数f(t)=的拉氏变换.

解

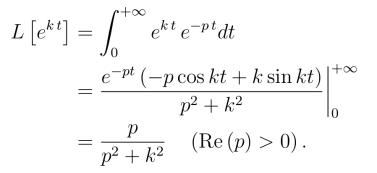
同理可求

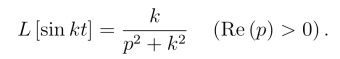
例4 求幂函数f(t)=tm 的拉氏变换（m为非负整数）

解 设(https://www.daowen.com)

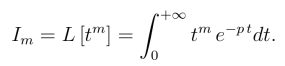
当m=0时,

当m ＞0时,由分部积分公式得

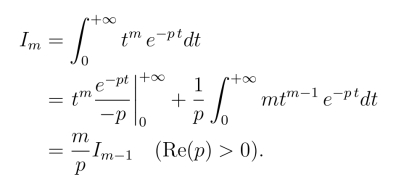
因此

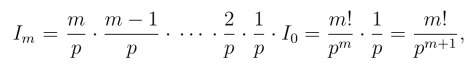
即

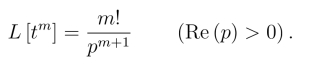
特别地,对实数m ＞-1,有

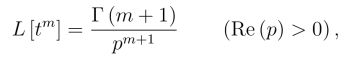
其中,Γ(·)为Γ(伽马)函数.

例5 设f(t)是以T为周期的周期函数,即f(t + T) = f(t)(t ＞0),在一个周期上分段连续,证明:

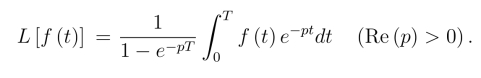
证明

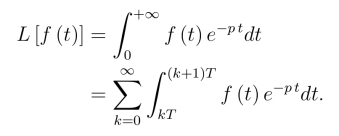
令t=u+kT,得