习题八
1.已知函数f(t)=tne-atu(t) ,则F (p)=L[f(t)] 的收敛域为_____.
(A) Re(p)＞a (B) Re(p)＞-a (C) Re(p)＞0 (D) Re(p)＜-a
2.下列函数中,增长不是指数级的是_____.
(A) et2 (B) u(t) (C) sin 2t (D) tn
3.设f(t)=tea t,则L[f(t)]=_____.
4.设f(t)=2δ(t)+e-tu(t-1),则L[f(t)]=_______.
5.设F (p)=
,则L-1[F (p)]=_____.
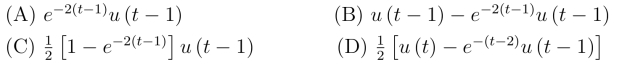
6.设f(t)=e-2t cos 3t ,则L[f(t)]=_____.
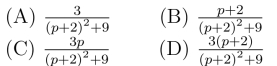
7.设L-1[1]=δ(t) ,则
=_____.
(A) δ(t)cos t (B) δ(t)-cos t
(C) δ(t)(1-sin t) (D) δ(t)-sin t
8.设F (p)=
则L-1[F (p)]=_____.
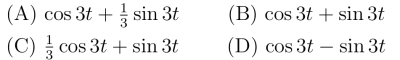
9.设F (p)=
,则L-1[F (p)]=_____.
(A) e-t sin 5t (B) -e-t sin 5t (C) -e-t cos 5t (D) e-t cos 5t
10.设F (p)=
则L-1[F (p)]=_____.
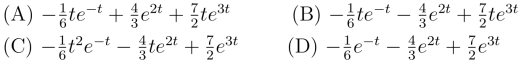
11.设f(t)=u(3t-6) ,则L[f(t)] =______________.
12.设L[f(t)]=
,则______________.
13.设F (p)=
,则L-1[F (p)] =______________.
14.设f(t)=(t-1)2et ,则L[f(t)] =______________.
15.设f(t)=2u(t-1)+3u(t-2),则L[f(t)] =______________.
16.
=______________.
17.若L[f′′(t)] = arccot p,且f(0) = 2,f′(0) = -1,则L[f(t)] =______________.
18.设L[f(t)]=F (p),则L[t3e5tf(t)] =______________.
19.
=______________.
20.已知L[f(t)]=F (p)=
则L[e-2tf(3t)] =______________.
21.利用定义求下列函数的拉氏变换：
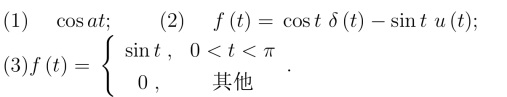
22.利用拉氏变换的线性性质及常用函数的拉氏变换,求下列函数的拉氏变换：q
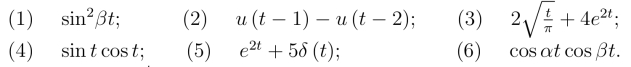
23.已知f(t)=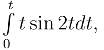
求L[f(t)]
24.计算
25.已知f(t)=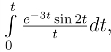
求L[f(t)]
26.计算下列积分
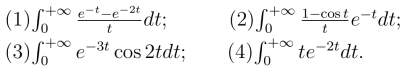
27.利用拉氏变换的性质,求下列函数的拉氏逆变换：
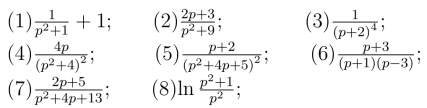
28.利用留数,求下列函数的拉氏逆变换：
29.求下列函数的拉氏逆变换：
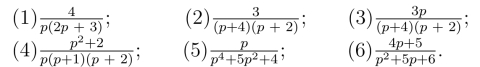
30.用卷积定理,求下列函数的拉氏逆变换：
31.求下列常微分方程的解：
(1) y′-y =e2t ,y(0)=0;
(2) y′′+4y =sin t,y(0)=y′(0)=0;
(3) y′′-y =4 sin t+5 cos 2t,y(0)=-1,y′(0)=-2;
(4) y′′+3y′+2y =u(t-1) ,y(0)=0,y′(0)=1;
(5) y′′+w2y =a[u(t)-u(t-b)] ,y(0)=0,y′(0)=0;
(6) y′′-y =0,y(0)=0,y(2π)=1.
32.求下列常微分方程组的解：
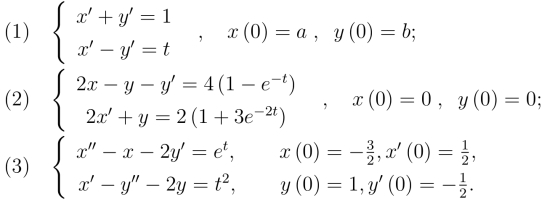
33.解下列微分积分方程：
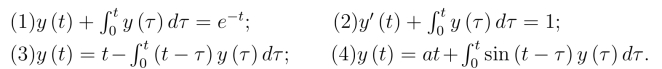
34.设L[f(t)]=F (p),a 为正常数,证明：
35.利用卷积证明