3.1.2 复积分存在的条件及计算公式
2026年01月14日
3.1.2 复积分存在的条件及计算公式
下面讨论积分式(3.1.1)在什么条件下存在.
函数f(z)=u(x,y)+iv(x,y)在D内处处连续,则u(x,y)及v(x,y)均为D内的连续函数.设ζk =ξk+iηk,由于
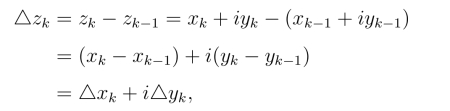
因此
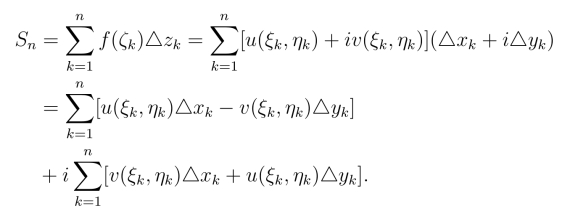
由于u,v都是连续函数,根据线积分的存在定理可知,当弧段长度的最大值趋于零时,不论对C的分法如何,点(ξk,ηk) 的取法如何,上式右端的两个和式的极限都是存在的.因此有
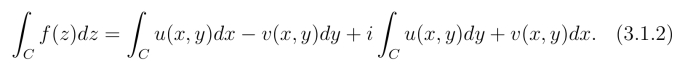
为便于记忆,公式(3.1.2)在形式上可以看作f(z) = u+iv与dz = dx+idy相乘后求积分得到,即
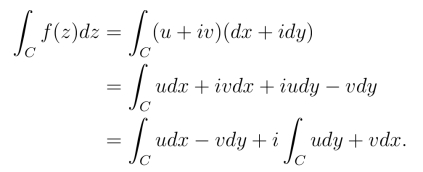
我们有下面结论:
定理(复积分存在的充分条件) 若C为光滑或逐段光滑的有向曲线段,f(z) 在C 上处处连续,则f(z)沿C 可积.
利用公式(3.1.2)可以计算函数f(z)沿曲线C的积分,可是需要计算两个二元实函数对坐标的曲线积分,通常很麻烦.下面对曲线C 为光滑曲线的情形,将该公式化为更简单的形式.
若C为有向光滑曲线,其参数方程为z =z(t)=x(t)+iy(t)(α ≤t ≤β),则z′(t)=x′(t)+iy′(t) 在区间[α,β]上连续且不等于零.
根据线积分的计算方法,有
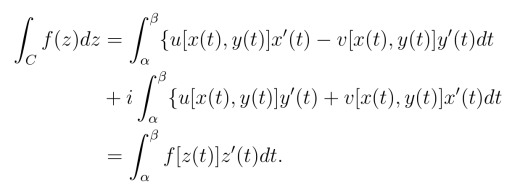
上式右端可以写成(https://www.daowen.com)
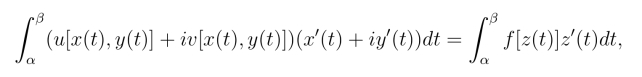
所以
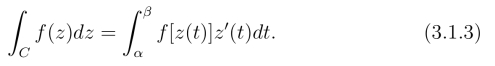
用公式(3.1.3)来计算复积分比较简便,该式可看作一般复积分的计算公式.
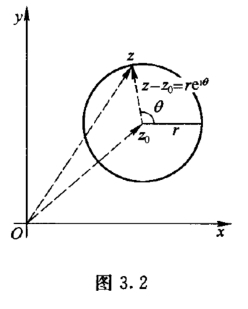
例1 设C为正向圆周|z-z0|=r(r >0),n为正整数,试证:
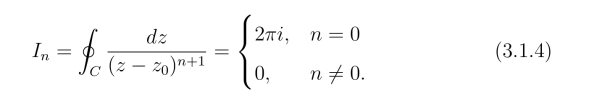
证明 C的方程写作z =z0+reiθ,0 ≤θ <2π(图3.2),所以
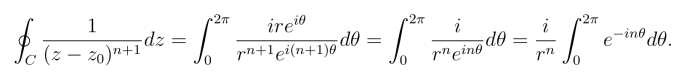
当n=0时得
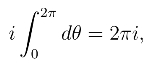
当n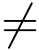 0时得
0时得
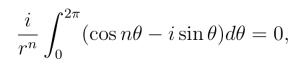
因此
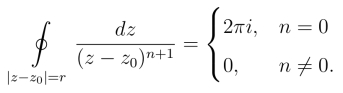
式(3.1.4)以后经常用到,可作为积分公式来使用,它的特点是积分值与积分路线圆周的中心和半径无关.
