1.3.2　简单曲线与光滑曲线

设复平面上的曲线C由参数方程z = x(t) + iy(t)(α ≤t ≤β)给出,x(t),y(t) 是区间[α,β]上的两个实变量连续函数,则称此曲线C为复平面上的一条连续曲线.

定义1 设曲线C :z =z(t)是[α,β]上的连续曲线,且对[α,β]上任意两个不同的点t1与t2(且不同时为[α,β]的端点),总有z(t1) 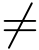z(t2),则称曲线C为简单曲线或若当曲线; z(α)和z(β)分别称为C的起点和终点,若简单曲线的起点与终点重合,则称它为简单闭曲线.

定义2 设曲线C的方程为z = z(t)(α ≤t ≤β),x′(t),y′(t) 在[α,β]上连续,且不全为零(即z′(t) 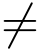0),则称曲线C : z = x(t)+iy(t)(α ≤t ≤β)为光滑曲线,由有限条光滑曲线依次首尾连接起来的曲线称为分段光滑曲线.

如直线、圆、椭圆等都是光滑曲线,而由有限条直线段连接成的折线是分段光滑的.