三、回归分析
回归分析和相关分析是一对紧密相关的分析方法,相关分析是进行回归分析的基础,在相关比较显著的时候,进行回归分析才有意义。如果相关的程度很低,进行回归分析就没有意义,因为那样计算出来的回归表达式没有代表性。回归分析是对相关分析的补充和延伸。相关分析只能计算出变量之间的相关程度,无法明确变量之间的因果关系,而回归分析可以对变量之间的因果关系进行探究。为了更好地探索家庭经济水平对本科生文化资本状况的影响,研究应进行回归分析。回归分析的结果让我们有可能对因变量进行基于自变量的预测。研究采用数据分析软件SPSS对数据进行回归分析。
(一)模型概要
如上Pearson相关分析表明,家庭经济水平与本科生文化资本状况呈正相关,为了进一步探究家庭经济水平对本科生文化资本状况可能存在的影响,研究采用了层次回归分析法进行多元线性回归,方法为逐步进入法,表2-14为运用相应的回归模型分析得出的回归结果。
表2-14 模型汇总
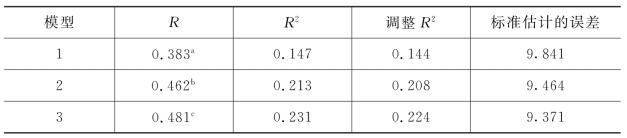
注:a.预测变量:(常量),SMEAN(N44耐用消费品)。
b.预测变量:(常量),SMEAN(N44耐用消费品),SMEAN(在校一年总支出)。
c.预测变量:(常量),SMEAN(N44耐用消费品),SMEAN(在校一年总支出),SMEAN(N42在校一年总支出家庭年总收入的比重)。
因变量:文化资本。
由表2-14可以看到R、R 2、调整的R 2和标准估计的误差这四个方面的数据。前面三个数据是为了告诉我们因变量可以被自变量预测的程度,最后一个值表示因变量不能被自变量解释的程度。
第一个值R是多元相关系数,它等于文化资本的原始值和通过回归分析得到的文化资本的预测值之间的相关系数的绝对值(0≤R≤1)。第二个值R 2是R的平方(0.4812=0.231),当乘以100%时,可理解为因变量的总变异性中被自变量解释的百分比。在研究中,自变量耐用消费品、在校一年总支出和在校一年总支出占家庭年总收入的比重揭示了本科生文化资本的总变异性的23.1%。调整的R 2是为了对总体值做更好的估计(基于样本计算的R 2容易高估总体值)。最后,标准估计的误差表明自变量不能预测因变量值的程度。标准估计的误差为9.371说明耐用消费品、在校一年总支出和在校一年总支出占家庭年总收入的比重三个自变量预测本科生的文化资本状况时,回归方程平均偏离约为9.371。
(二)方差分析——检验回归的整体显著性
表2-15用来检验包含所有预测变量的回归模型预测本科生文化资本状况的显著性。在表格中,p值小于或等于0.05说明包含所有预测变量的回归模型能够显著地预测本科生的文化资本状况。因为p值(0.000)是小于0.05的,所以原假设R 2=0被拒绝,说明回归方程(包含三个预测变量)预测本科生的文化资本状况具有显著性。
表2-15 方差分析
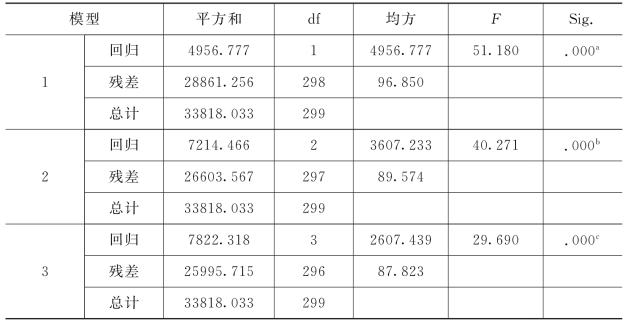
注:a.预测变量:(常量),SMEAN(N44耐用消费品)。
b.预测变量:(常量),SMEAN(N44耐用消费品),SMEAN(在校一年总支出)。
c.预测变量:(常量),SMEAN(N44耐用消费品),SMEAN(在校一年总支出),SMEAN(N42在校一年总支出占家庭年总收入的比重)。
因变量:文化资本状况。
(三)系数——检验单个预测变量的显著性
表2-16提供了构建回归方程和检验每个预测变量显著性的必要值。在多元回归中,方程以下面的形式建立:
![]()
式中,Y——因变量的预测值,即本科生文化资本的预测值;
a——Y轴截距,即当所有的Xs为0时Y的值;
b——第i个预测变量的回归系数,在研究中,i的取值为1、2、3,依次表示第一个变量(耐用消费品)、第二个变量(在校一年总支出)和第三个变量(在校一年总支出占家庭年总收入的比重);
Xi——每一个参与者第i个自变量的取值,在研究中,i的取值为1、2、3,以此表示第一个自变量、第二个自变量和第三个自变量。
回归方程中的a(Y轴截距;在SPSS中称为常数)和b1,b2,b 3(每个自变量的回归系数)可以在上表非标准化系数中找到。Y轴截距的取值为36.542,耐用消费品、在校一年总支出和在校一年总支出占家庭年总收入的比重的系数分别是2.702、2.517和1.476。将这些值代入回归方程中,我们可以得到如下所示的预测本科生文化资本状况的方程:
Y本科生文化资本=36.542+2.702(耐用消费品)+2.507(在校一年总支出)+1.476(在校一年总支出占家庭年总收入的比重)
表2-16 系数
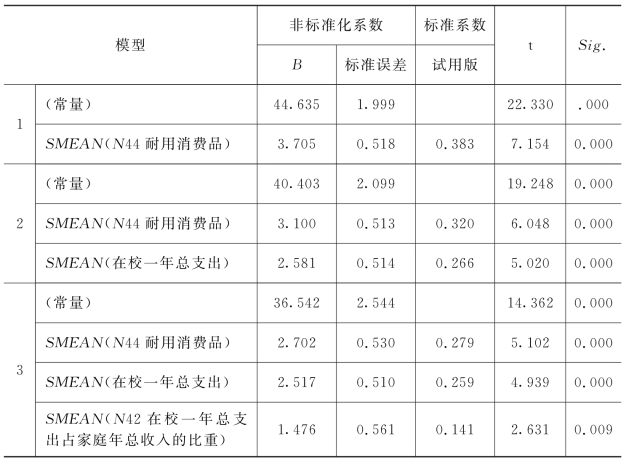
注:因变量为文化资本状况。
这里可以以一位家庭所在地为农村的本科生的数据为例,对这三个自变量分别给定一个取值,就可以得到一个文化资本状况的预测值。譬如,第一个参与者的家庭人均纯收入、住房条件和家庭经济主要来源的取值分别为5、2和5,将这些数代入方程得到文化资本状况的一个预测值:
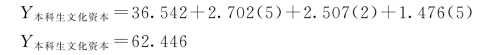
使用这一方程可以求出数据库中每个人的预测值。但是测试大多会有些误差(它们一般不会刚好等于真实值);R值越大,预测值越接近真实值,R=1.0就能得到完美的预测(预测值与实际值完全一致)。
