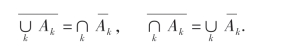事件的关系及运算
在实际问题中，往往要求我们在一个随机试验下同时研究几个事件及它们之间的联系.下面对应着集合的关系和运算来定义事件的关系和运算，并根据“事件发生”的含义，给出它们在概率论中的含义.
设随机试验的样本空间为Ω，随机事件A，B，Ak，Bk（k=1，2，3，…，n，…）都是Ω的子集.
（1）如果事件A中的每一个样本点都属于事件B，则称事件B包含事件A，或称事件A被包含于事件B，记作A⊂B或B⊃A.事件B包含事件A的含义是：事件A发生必然导致事件B发生.显然，对任一事件A有
（2）如果A⊂B，同时B⊂A，则称事件A与B相等（即两集合相等），记作A=B.
（3）由至少属于A，B两事件之一的一切样本点组成的集合，称为A与B的和（并），记为A∪B.事件A∪B发生当且仅当事件A发生或事件B发生.因此，通常也把事件A∪B表述为“事件A发生或事件B发生”，或表述为“事件A与B至少有一个发生”.
（4）同时属于事件A和B的所有样本点组成的集合，称为A与B的积（交），记作A∩B或AB.事件AB发生当且仅当事件A，B同时发生，所以常常将事件AB表述为“事件A和B同时发生”.
由上述定义和集合的运算规律可知，对任意两个事件A，B，若A⊂B，则必有
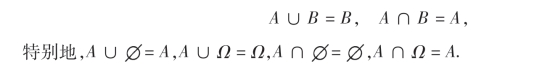
（5）如果A∩B=
，则称事件A，B是互不相容的或互斥的.互不相容的两事件不可能在一次试验中同时发生.基本事件是两两互不相容的.
（6）由属于事件A但不属于事件B的样本点组成的集合，称为事件A与B的差，记作A-B.当且仅当A发生、B不发生时，事件A-B发生.有时也将事件A-B表述为“事件A发生而事件B不发生”.显然
此外，由对立事件的定义得知：
事件的和与积的运算可以推广到有限个甚至可列无限多个事件的情形：
上面我们利用集合论的概念引入了概率论的一些基本概念，为了便于对照，列成下表：
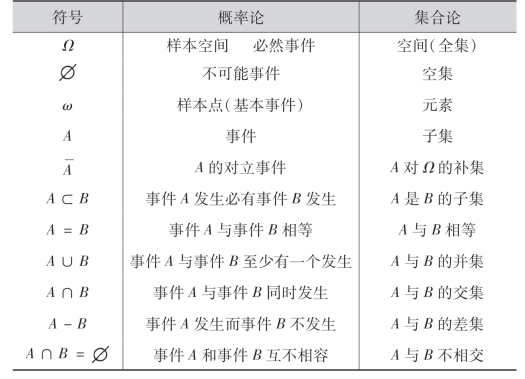
由于事件、事件的关系及运算与集合、集合的关系及运算是相当的，所以根据集合的运算性质可推得事件的运算性质如下：
（i）交换律：
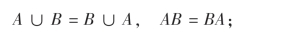
（ii）结合律：
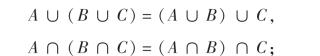
（iii）分配律：
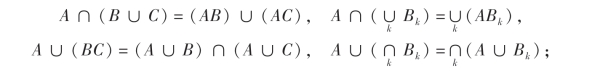
（iv）对偶律：对有限个或可列无限多个Ak，恒有
