二、矩估计法
在概率论中，某些总体分布的参数与它的矩是一致的，如正态分布X～N（μ，σ2）的参数μ和σ2就是总体的均值和方差，泊松分布X～π（λ）中参数λ就是总体的均值；有些总体分布的参数虽然与它的矩不是一致关系，但存在函数关系，如指数分布的均值为
.所以在对总体的参数做点估计时，首先想到用样本矩来估计相应的总体矩；当总体分布的参数与它的矩不一致时，如果总体中有k个未知参数，只要用前k阶样本矩来估计相应的前k阶总体矩，然后利用未知参数和总体矩之间的函数关系来求得参数的估计量.这种以样本矩估计相应总体矩来求出未知参数的估计量的方法称为矩估计法.
矩估计法是较早提出的求参数点估计的方法，其理论基础是：若总体X的k阶矩E（Xk）=μk（k≥1）存在，则当样本容量n→∞时，样本k阶矩依概率收敛于总体的相应的k阶矩，样本矩的连续函数依概率收敛于相应总体矩的连续函数.所以我们就用样本矩作为相应的总体矩的估计量，以样本矩的连续函数作为相应的总体矩的连续函数的估计量.
定义2 假设总体X的分布函数中含有k个未知参数θ1，θ2，…，θk，即F=F（x；θ1，θ2，…，θk），总体X的前k阶矩μl=E（Xl）（l=1，2，…，k）存在，它们是θ1，θ2，…，θk的函数μl（θ1，θ2，…，θk），l=1，2，…，k；又假设X1，X2，…，Xn是总体X的一个样本，可建立统计量——样本l阶原点矩Al，l=1，2，…，k，由下列方程组：
例2 设总体X在［a，b］上服从均匀分布，a，b为未知，X1，X2，…，Xn是X的一个样本，试求a，b的矩估计量.
解
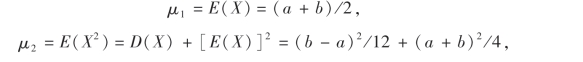
令
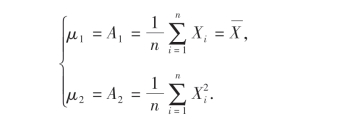
即
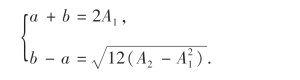
解之得a，b的矩估计量分别为
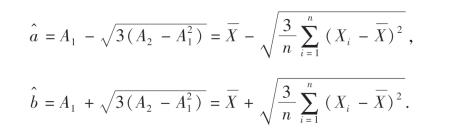
例3 设总体X的均值E（X）=μ及方差D（X）=σ2都存在，且σ2＞0，但μ，σ2均未知，又设X1，X2，…，Xn是一个样本，试求μ，σ2的矩估计量.
解
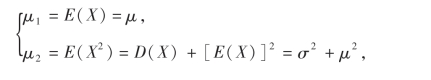
令
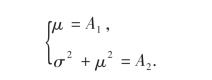
解此以μ，σ2为未知量的方程组，得到μ，σ2的矩估计量分别为
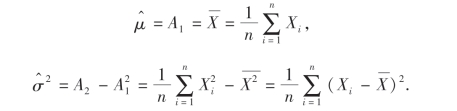
所得结果表明，总体均值与方差的矩估计量的表达式不因不同的总体分布而异.
例4 设总体X服从自由度为α，β的Γ分布，即X ～Γ（α，β），其概率密度为
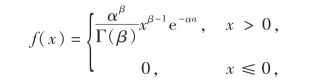
其中α ＞0，β＞0，均为常数，试求α及β的矩估计量.
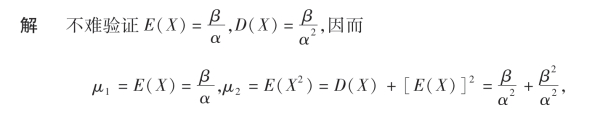
令
矩估计法既直观又很简便，特别是在对总体的数学期望与方差数字特征作估计时，并不一定要知道X的分布函数F（x，θ）.但是矩估计法要求随机变量的原点矩存在，而有的分布的原点矩不存在（如哥西分布），那就不能用矩估计法了；再者，矩估计法产生的估计量往往不够理想，这是因为样本矩的表达式同总体的分布函数的表达式无关，矩估计法便没有充分利用总体对参数所提供的信息，所以英国数学家费歇（R.A.Fisher）引入了较矩估计法为优的极大似然估计法.