频率和统计规律性
在讨论随机试验的时候，常常需要了解某些事件在一次试验中发生的可能性的大小，以便掌握随机现象的内在规律.为了研究这个问题，我们先引进频率的概念.
将随机试验重复进行N次，若事件A在这N次试验中发生了n次，则称
为事件A在这N次试验中发生的频率.
根据定义容易验证频率具有如下性质：
（1）对任一事件A，有
（2）FN（Ω）=1；
（3）若A1，A2，…，Ak是两两互不相容的事件，则
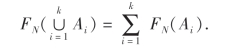
由于在任意N次试验中，事件A发生的次数具有偶然性，故A发生的频率FN（A）也具有不确定性.那么，由事件A发生的频率能否发现事件A发生的规律？为此，有许多人做了这样的试验.
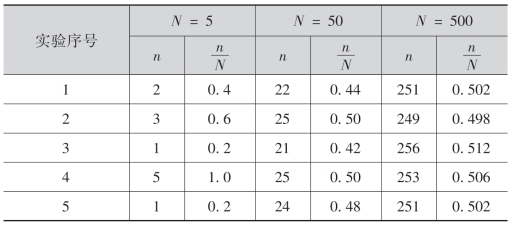
例如，考虑“掷一枚均匀的硬币，观察其正、反面出现的情况”这一随机试验.将硬币抛掷5次、50次、500次，各做10遍.其结果记录在下表里，表中N表示投掷次数，n表示出现正面朝上的次数，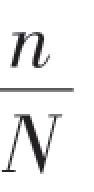
是事件“正面朝上”发生的频率.
从下表可以看出，虽然对于同样的试验次数，但事件“正面朝上”的频率却不尽相同，即具有随机波动性.随着试验次数的增加，该事件发生的频率在数值0.5附近摆动而呈现出一种稳定性.
续表
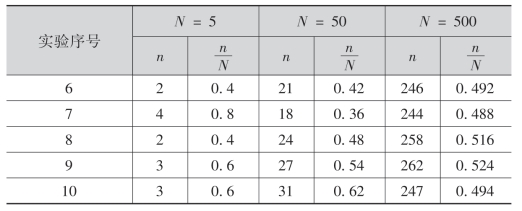
又如，为了观察“由0，1，2，…，9十个数字中任意取出一个数字”的随机试验中，事件“取出的数字是1”发生的规律，利用电子计算机进行模拟试验.下表列出10个2000次的观察结果.
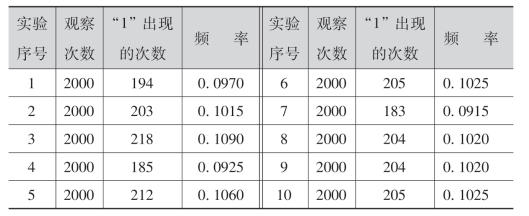
从上表可知，事件“取出的数字是1”发生的频率稳定在0.10附近摆动.
从上面两个例子可以看到，在重复试验中，同一事件发生的频率不完全相同，当试验次数较小时，频率的波动幅度较大；而当试验次数逐渐增大时，频率逐渐稳定于某一常数.频率的这种稳定性，即通常所说的统计规律性，说明了一个事件发生的可能性有一定的大小可言.当频率稳定于较大的数值，表明相应事件发生的可能性大；当频率稳定于较小的数值，表明相应事件发生的可能性小，而频率所稳定的数值就是相应事件发生可能性大小的一个客观的定量的度量，称为相应事件的统计概率，简称为概率.
定义1 设在同一组条件下，重复进行了N次随机试验.当N很大时，某一随机事件A发生的频率FN（A）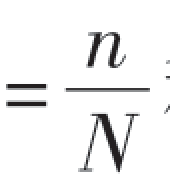
稳定地在某一常数p的附近摆动，则称该常数p（频率的摆动中心）为随机事件A的概率，记作
统计概率的定义中，虽然没有提供直接确定概率的方法，但是当试验次数较大时，事件A发生的频率可以作为P（A）的一个估计值.
由频率的性质，我们可以得出统计概率的性质：
（1）非负性：对任一事件A，有
（2）规范性：对必然事件Ω，有
（3）有限可加性：若事件A1，A2，…，An两两互不相容，则
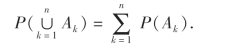
用概率的统计定义来确定某一事件A的概率P（A），往往要进行大量的试验.尽管如此，还是保证不了一定能得到P（A）的精确值.
在某些特殊的情况下，不需要进行大量的试验，而根据问题本身所具有的某种“对称性”，分析事件自身的特点，就可以直接计算其概率.这就是下面将要介绍的古典概型和几何概率.