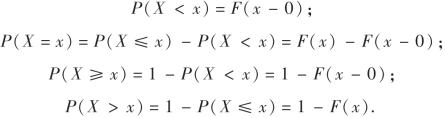二、分布函数

二、分布函数

定义2 设X是一个随机变量.对任意实数x，事件｛X≤x｝的概率P（X≤x）称为随机变量X的分布函数，记作F（x），即

分布函数是一个普通的函数，即实变量实值函数，有了分布函数概念后，我们就能利用高等数学的知识来研究随机变量.

由定义易知，对任意实数x有：0≤F（x）≤1.如果知道随机变量X的分布函数F（x），就能算出X落入某区间（x1，x2］（x1＜x2）的概率P（x1＜X≤x2）.因为

且

故有

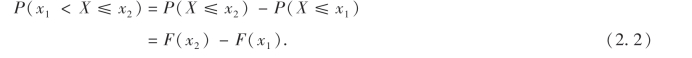
下面给出随机变量X的分布函数的基本性质.

（1）F（x）是x的不减函数：若x1＜x2，则F（x1）≤F（x2）；

（3）F（x）在任一点右连续：F（x+0）=F（x）.

性质（1）可由式（2.2）直接推得.性质（2）和性质（3）证略.对于性质（2），我们可以这样理解：当x逐渐增大而趋于无穷大时，｛X≤x｝愈来愈接近于必然事件，因此函数F（x），即事件｛X≤x｝的概率趋于必然事件的概率，也就是说.用类似的方法可说明

可以证明，满足上述三个性质的函数必是某随机变量的分布函数.

设F（x）是随机变量X的分布函数.为了便于计算X在某些范围内取值的概率，下面再给出几个公式：