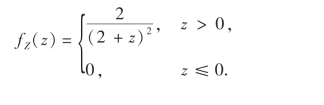二、Z=的分布

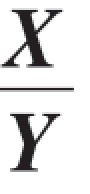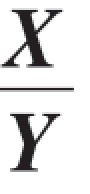二、Z= 的分布

以下我们仅对二维随机变量（X，Y）是连续型的情形进行探讨，离散型的情形跟和的分布的求法一致.

设（X，Y）是二维连续型随机变量，其概率密度为f（x，y），则Z=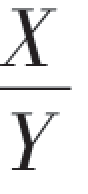的分布函数为

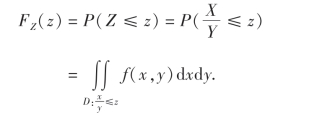
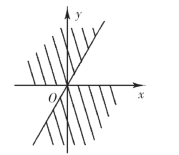
图3-7

其中积分区域D为图3-7中所示的阴影部分，化为二次积分得

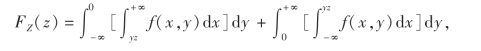
令x=yu，并交换积分次序得

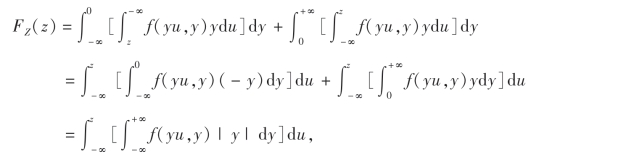
于是得Z的概率密度为

特别地，如果X和Y相互独立，（3.28）式可写成

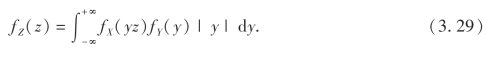
例15 设X和Y是两个相互独立的随机变量，它们的概率密度分别为

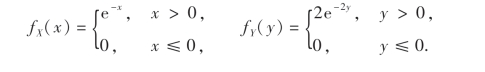
求Z=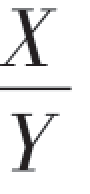的概率密度.

解 由（3.29）式，Z的概率密度为

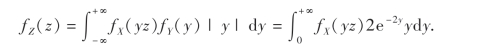
上面的积分中y＞0，所以

当z≤0时，yz≤0，有fX（yz）=0， fZ（z）=0.

当z＞0时，yz＞0，fX（yz）=e-yz，此时

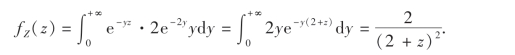
故所求Z的概率密度为