单个正态总体X ～N（μ，σ2）的区间估计
假设总体X～N（μ，σ2），X1，X2，…，Xn是来自总体X的容量为n的样本，我们分别对总体均值μ和总体方差σ2的区间估计进行讨论.
1.总体均值μ的置信区间
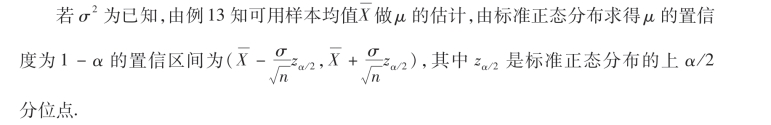
例14 已知晶体管收音机的磁棒长度服从正态分布，从生产车间某日的产品中随机抽取6根，测得长度如下（单位：厘米）：
已知当天产品长度的标准方差为σ=0.25，试找出平均长度的置信区间（置信度1-α=0.95）.
解 因为样本均值X的观测值
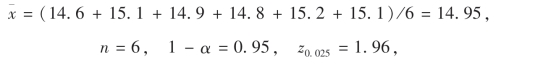
代入（7.11）式，平均长度的置信度为0.95的置信区间是
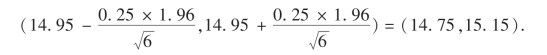
其中S2是样本方差，而右边的t分布不依赖任何参数（参看图7-2），此时对于给定的1-α，存在tα/2（n-1），使得
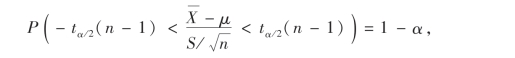
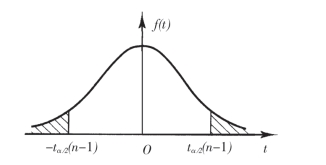
图7-2
即
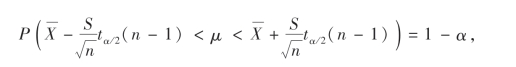
求得μ的置信度为1-α的置信区间就是
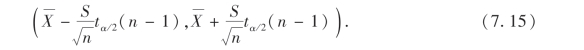
例15 某种布匹的重量服从正态分布，现从产品中抽得容量为16的样本，测得重量如下：
求布匹平均重量的置信度为95%的置信区间.
解 设布匹重量X ～N（μ，σ2），σ2未知，由于n=16，¯x=77.7/16=4.856，S2=0.04，t0.025（15）=2.131，于是布匹平均重量的置信度为95%的置信区间为
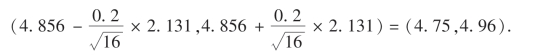
2.总体方差σ2的置信区间
根据实际问题的需要，此处只介绍μ未知时方差σ2的置信区间.已经知道样本方差S2是σ2的无偏估计，根据第六章的定理有
显然χ2（n-1）分布不含任何未知参数.给定置信度1-α（0＜α＜1），存在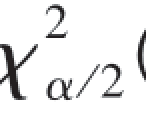
（n-1）和
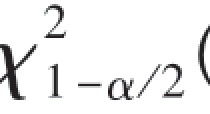（n-1）使得（图7-3）
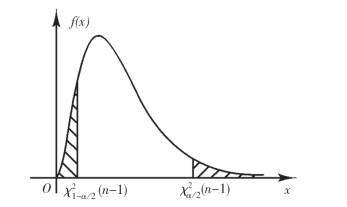
图7-3
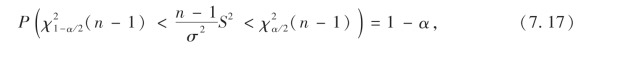
所以
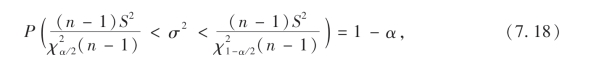
可得方差σ2的置信度为1-α置信区间为
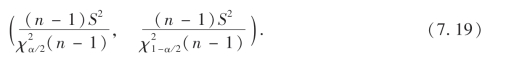
注意，虽然χ2分布和F分布的密度函数是不对称的，但我们仍然像对待标准正态分布、t分布那样取对称的分位点来确定置信区间.
例16 生活中常用投资的回收利润率来衡量投资风险，现随机地调查了26项年回收利润率（%），得到样本标准差S=15（%）.设回收利润率服从正态分布，试求方差σ2的置信度为0.95的置信区间.
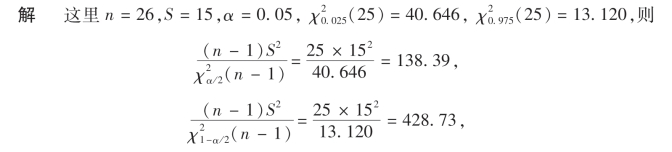
所以σ2的置信度为0.95的置信区间为（138.39，428.73）.
例17 为了确定某种溶液中的甲醛浓度，取得4个独立的实测值的平均值¯x=8.34%，样本的标准差s=0.03%，现已知甲醛浓度服从正态分布，求总体标准差σ的置信度为95%的置信区间.
解 这里n=4，¯x=8.34%，s=0.03%.
即标准差σ的置信度为1-α的一个置信区间为
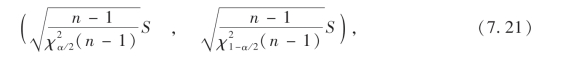
得σ（标准差）的置信度为95%的一个置信区间为（0.017%，0.112%）.