数学期望的性质
数学期望在理论和应用上都极为重要,下面给出它的几个常用性质,若能熟练地掌握这些性质,在某些情况下,可大大降低计算的难度和复杂性.
性质1 若C为常数,则有E(C)=C.
证 因为常量C作为随机变量而言,是一个离散型随机变量,它只有一个可能值C,概率为1,根据(4.1)式,得
![]()
性质2 若X是随机变量,a,b是常数,则
![]()
证 设X为连续型随机变量,概率密度函数为f(x),则根据(4.4)式,得
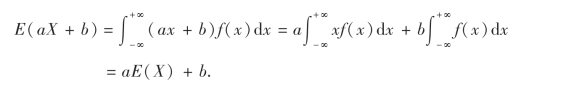
性质3 若X,Y是任意两个随机变量,则有
![]()
证 设(X,Y)为连续型随机变量,其联合概率密度为f(x,y),则根据(4.6)式,得
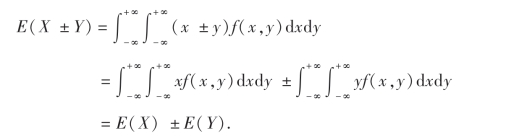
性质4 若随机变量X和Y相互独立,则
![]()
证 设(X,Y)为连续型随机变量,其联合概率密度为f(x,y),边缘概率密度为fX(x),fY(y),根据X和Y相互独立性,由(4.6)式,得
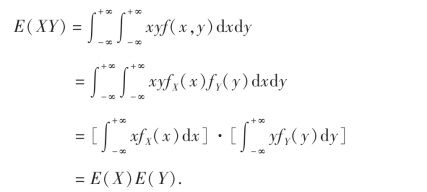
性质2,3,4可推广到有限个随机变量的场合(这里的证明仅对连续型给出,离散型的证明与之类似,读者可自行证明).
性质5 若X≥0,则E(X)≥0;若X1≥X2,则
![]()
证 当X≥0时,由(4.1)式可知E(X)≥0.
若X1≥X2,则X1-X2≥0,从而E(X1-X2)≥0,即
![]()
故
![]()
性质6 |E(X)|≤E(|X|).
证 因为-|X|≤X≤|X|,由性质5知
![]()
从而
![]()
性质7 柯西-许瓦兹不等式:若E(X2),E(Y2)均存在,则E(XY)存在,且
![]()
证 考虑实变量t的二次函数
![]()
根据性质5对一切t,均有g(t)≥0,由一元二次方程有实根的判别条件,有
![]()
即
![]()
例8 设随机变量X ~B(n,p),求E(X).
解 前面我们已经由(4.1)式求得E(X)=np,以下我们利用性质3来计算E(X).
引入随机变量

则X1,X2,…,Xn相互独立,且X=X1+X2+… +Xn服从二项分布.
由于Xi服从二点分布,则
![]()
根据数学期望性质3得
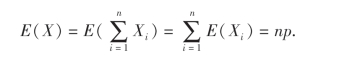
例9 袋中有n张卡片,号码分别为1,2,…,n,从中有放回地抽出k张卡片,求这k张卡片的号码之和X的数学期望.,

故
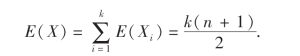
注:在上面两例中,我们都是把一个比较复杂的随机变量X拆成n个比较简单的随机变量Xi(如例8Xi服从二点分布,例9Xi虽不服从二点分布,但其概率分布易求)之和,然后根据数学期望的性质,把这些简单的随机变量Xi的数学期望相加即可得到X的数学期望,这种处理方法巧妙方便,具有一定的普遍意义,不失为一种好方法.
