一、数学模型

一、数学模型

设影响试验指标的两个因子为A，B，其中，因子A有r个水平：A1，A2，…，Ar；因子B有s个水平：B1，B2，…，Bs.在每种水平组合AiBj下均重复做t次试验，试验结果如下表所示：

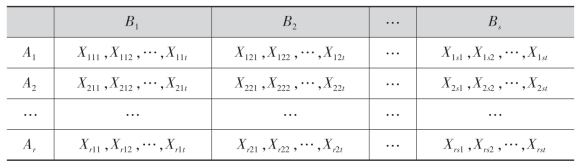
设在水平组合AiBj下的试验指标Xij～N（μij，σ2），则Xij1，Xij2，…，Xijt就是Xij的一个样本，并设这些样本是相互独立的，而μij和σ2均为未知参数，这样即有Xijk～N（μij，σ2），各Xijk相互独立，i=1，2，…，r；j=1，2，…，s；k=1，2，…，t.

引进随机误差εijk，则有以下表示：

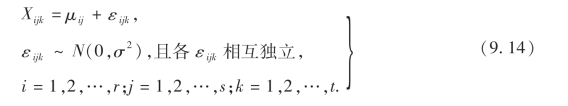
现在我们要判断因子A与因子B对试验指标有无显著性影响，为使问题变得更清楚，将μij排成下表.

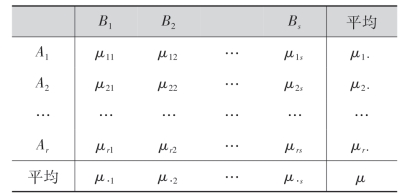
其中

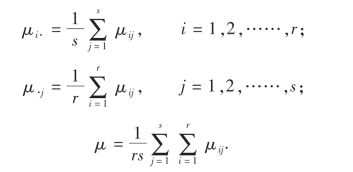
μ·j表示当B取水平Bj时，A从水平A1变化到Ar时各总体X1j，X2j，…，Xrj的均值的平均值，我们称μ·j为水平Bj的均值.μi·表示当A取水平Ai时，B从水平B1变化到Bs时各总体Xi1，Xi2，…，Xis的均值的平均值，称μi·为水平Ai的均值，μ称为总均值.

令 αi=μi·-μ， i=1，2，…，r；

βj=μ·j-μ， j=1，2，…，s.

在双因子试验中，一般把因子A与B的交互效应设想为某一个因子的效应，该因子记为A×B，并称为A与B对试验指标的交互作用.

由（9.15）知：μij=μ+αi+βj+γij，则有

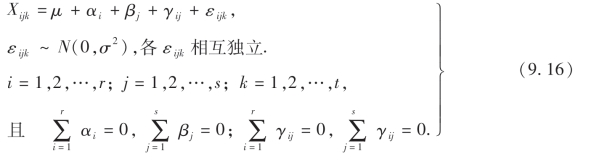
其中αi，βj，μ，γij是未知参数.

我们所提的问题化为检验以下三个假设：

而（9.16）式就是双因子方差分析的数学模型.