三、参数估计

三、参数估计

在方差分析模型中，我们假设了在水平Aj下的试验指标Xj～N（μj，σ2），这里μj，σ2均为未知参数，下面给出它们的估计.

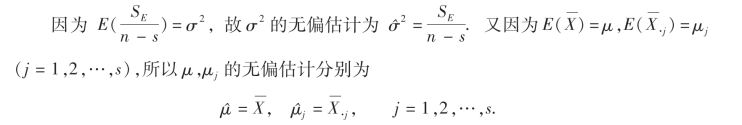
当否定H0时，意味着水平效应δ1，δ2，…，δs不全为零，这时需对δj（j=1，2，…，s）做出估计.因为δj=μj-μ，j=1，2，…，s，所以δj的无偏估计为

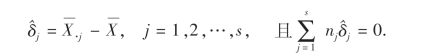
在实际问题中，如果检验结果是否定假设H0，此时，自然还希望能进一步确定因子A取什么水平时效果最佳，这就需要对两个不同水平下的均值进行比较.即考察两个总体Xj与Xk（j≠k）的均值差μj-μk，并对它们做出置信度为1-α的区间估计.若置信区间包含0，则说明μj与μk之间无显著性差异；否则说明存在显著性差异.具体做法如下：

即

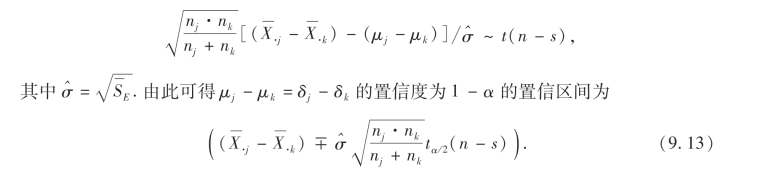
例5 求例3中的未知参数σ2及每种农药的杀虫率均值和效应μj，δj（j=1，2，…，6）的估计及均值差的置信度为0.95的置信区间.

解

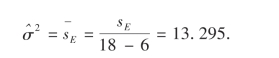
各种农药杀虫率的均值的估计依次为

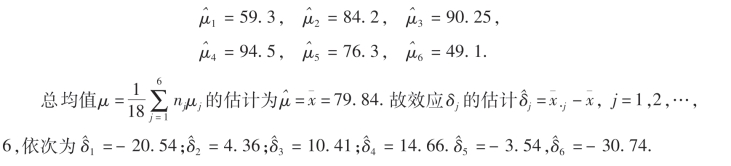
由于有6个均值，可以有15个均值差，这里我们只求其中一个均值差的置信区间，比如μ4-μ3的置信区间求解如下：

因为α=0.05，n=18，s=6，n3=n4=4.查表得

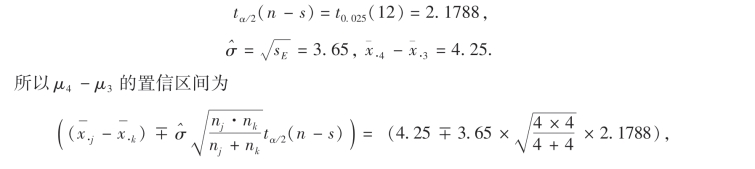
即（-1.38，9.88）.由于置信区间包含0，因而表明μ3与μ4之间无显著差异，即农药Ⅲ与Ⅳ的效果相当.