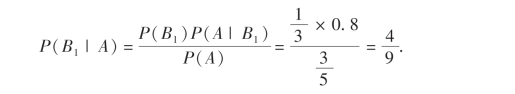贝叶斯(Bayes)公式
假设在某随机试验中,事件A的发生受到许多因素的影响,即存在一事件组B1,B2,…,Bn,其中B1,B2,…,Bn互不相容,使得当且仅当B1,B2,…,Bn中的任一事件发生时,A才可能发生.如果在试验之前,根据某些理由可确定Bi的概率P(Bi)(试验前的假设概率)及P(A|Bi)(i=1,2,…,n).现在进行一次试验,而事件A的确发生了,因此需对事件Bi的概率给予重新估计,即要计算事件Bi在事件A已发生的条件下的条件概率P(Bi|A)(试验后的假设概率).

其中k=1,2,…,n.
(1.19)式称为贝叶斯(Bayes)公式.
证 从条件概率的定义可得
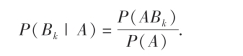
根据乘法定理和全概率公式分别得到
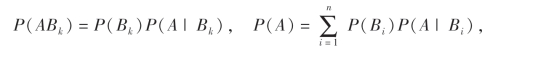
故
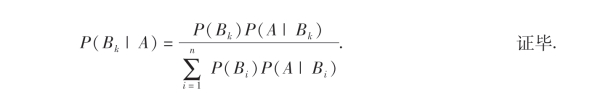
在实际问题中,贝叶斯公式适用于试验之后,求解导致某事件发生的各种“原因”的概率.
例22 某射击小组共有20名射手,其中一级射手4人,二级射手8人,三级射手7人,四级射手1人.一、二、三、四级射手能通过选拔进入比赛的概率分别是0.9,0.7,0.5,0.2.现从该射击小组任选一人,若此人已通过选拔进入比赛,问此人是一级射手的概率等于多少?
解 设A表示事件“任选的一名射手能通过选拔进入比赛”,Bi表示事件“任选的一名射手是i级射手”,i=1,2,3,4.显然B1,B2,B3,B4是样本空间的一个划分.由题设条件知
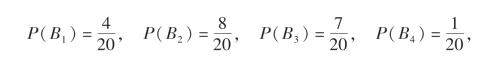
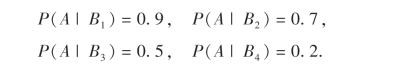
所求概率为P(B1|A),由贝叶斯公式

例23 某大学生准备参加毕业论文答辩,答辩的效果与他的精神状态有关.据他估计,如果他的精神状态很好的话,则答辩通过的概率为0.8;若精神状态一般的话,则通过的概率为0.6;若精神状态很差的话,则通过的概率降为0.4.该生感到他的精神状态处于“很好”“一般”或“很差”都是等可能的.
(1)试求他通过毕业论文答辩的概率;(2)现在已知他通过了这次论文答辩,求他答辩时,精神状态处于“很好”的概率.解 设A表示事件“他通过论文答辩”,B1,B2和B3分别表示他的精神状态处于“很好”“一般”和“很差”这三个事件.显然,B1,B2,B3是样本空间Ω的一个划分,且
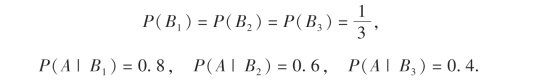
(1)由全概率公式知
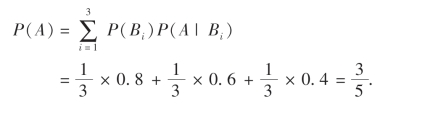
(2)由贝叶斯公式得