§5.3 中心极限定理
我们曾特别强调了正态分布在概率论与数理统计中的地位与作用.为什么客观实际中许多随机变量服从正态分布？是经验猜测还是确有科学的理论依据，下面我们就来解释这一问题.
我们已经知道，炮弹的弹着点射击误差服从正态分布，我们来分析其原因.要知道误差是什么样的随机变量，有必要研究一下造成误差的原因是什么？ 每次射击后，炮弹会因为震动而造成很微小的偏差X1，炮弹外形细小的差别而引起空气阻力不同而出现的误差X2，炮弹前进时遇到的空气流的微小扰动而造成的误差X3，等等，有许多原因，每种原因引起一个微小的误差都是随机的，而弹着点的总误差X是许多随机误差的总和，即X=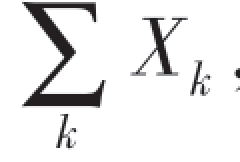
，而且Xk之间可以看成相互独立的，因此要讨论X的分布就要讨论这些相互独立的随机变量之和的分布.
在概率论中，我们把研究在一定条件下，大量独立随机变量和的极限的分布是正态分布的那些定理通常叫作中心极限定理.本节只介绍两个条件简单，也较常用的中心极限定理.
定理4（同分布中心极限定理） 设随机变量X1，X2，…，Xn，… 相互独立，服从同一分布，且具有有限的数学期望和方差，E（Xk）=μ，D（Xk）=σ2＞0（k=1，2，…）则随机变量
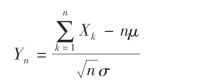
的分布函数Fn（x）对任意的x，满足
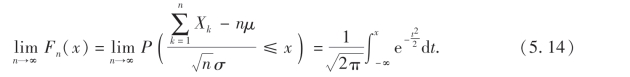
证略.该定理常称作列维定理.
其中x1，x2是任意实数.
由定理4可以得到另一个重要定理.
定理5（德莫弗-拉普拉斯定理） 设随机变量ηn（n=1，2，3，…）服从具有参数n，p（0＜p＜1）的二项分布，则有
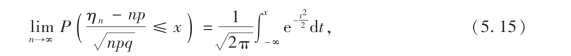
其中x为任意实数，p+q=1.
证略.
定理5告诉我们，若随机变量ηn服从二项分布B（n，p），则当n充分大时，ηn将近似服从正态分布N（np，npq），且定理5有下面两个常用形式：其中ηn为n次独立试验中事件A出现的次数，每次试验中事件A出现的概率为p.下面举几个应用中心极限定理的例子.
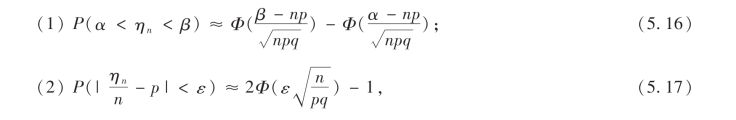
例1 假设生产线上组装每件成品的时间服从指数分布，统计资料表明该生产线每件成品的组装时间为10分钟，各件产品的组装时间相互独立.试求组装100件成品需要15个小时到20个小时的概率.
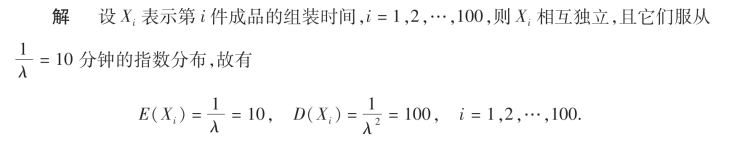
由于n=100较大，由定理4知所求概率为
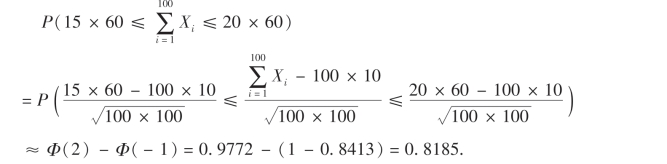
所以组装100件成品，需要15个小时至20个小时的概率是0.8185.
例2 某单位内部有260架电话分机，每个分机有4%的时间要用外线通话，可以认为各个电话分机用不用外线是相互独立的，问总机要多少条外线才能以95%的把握保证各个分机在用外线时不必等候.
解 把考察每部电话分机是否使用外线作为一次独立的试验，用｛Xk=1｝表示第k部电话分机使用外线这一事件，而｛Xk=0｝表示第k部电话分机不使用外线，即
据题意要确定最小的整数x，使得
成立.因为n=260较大，所以由定理5有
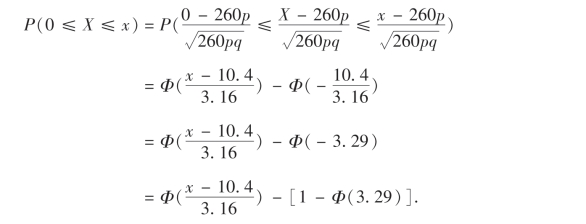
因为Φ（3.29）≈0.9995，所以
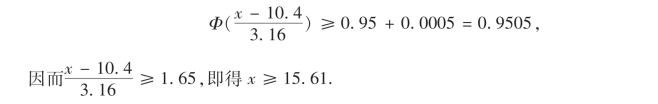
取最接近的整数x=16，所以总机至少应备有16条外线，才能有95%以上的把握保证各个分机在使用外线时不必等候.
例3 数值计算时，任何数x都只能用一定位数的有限小数y来近似表示，这就产生了一个误差ε=x-y.在下面的讨论中，我们假定参加运算的数都用十进制定点表示，每个数都用四舍五入的方法取到小数点后五位，这时相应的舍入误差可以看作是［-0.5×10-5，0.5×10-5］上的均匀分布.现在如果要求n个数xi（i=1，2，…，n）的和S，在数值计算中就只能求出相应的有限小数yi（i=1，2，…，n）的和T，并用T作为S的近似值.自然要问，这样做造成的误差η=S-T是多少？
解 因为
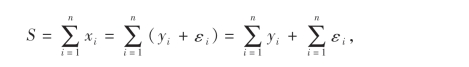
故
若n=10000，则
中心极限定理的内容包含极限，因而称它为极限定理是很自然的，由于大量随机变量和的极限分布是正态分布这一课题自18世纪开始的长达2个世纪的时期内概率论研究的中心课题，且由于它在统计等领域中的重要性，因而波利亚（Polya）于1920年给它取名为“中心极限定理”.